A plant virus is found to consist of uniform cylindrical particle of 150Å in diameter 5000 Å long. The specific volume of the virus is 0.75 mLg−1. If the virus is considered to be a single particle, find its molar mass.
The correct Answer is:7.09×107
To find the molar mass of the plant virus, we can follow these steps:
Step 1: Calculate the Volume of the Virus
The virus is modeled as a cylinder. The volume V of a cylinder is given by the formula:
V=πr2h
Where:
- r is the radius of the cylinder
- h is the height (length) of the cylinder
Given:
- Diameter = 150 Å, so radius r=1502=75 Å
- Length h=5000 Å
First, convert the dimensions from angstroms to centimeters:
- 1 Å=10−8 cm
- Radius r=75×10−8 cm
- Height h=5000×10−8 cm
Now, calculate the volume:
V=π(75×10−8)2(5000×10−8)
V=π(5.625×10−15)(5.0×10−5)
V=π(2.8125×10−20) cm3
V≈8.83×10−20 cm3
Step 2: Calculate the Mass of the Virus
Using the specific volume v=0.75 mL/g (which is equivalent to 0.75 cm3/g), we can find the mass m using the formula:
m=Vv
Substituting the values:
m=8.83×10−200.75
m≈1.1773×10−19 g
Step 3: Calculate the Molar Mass
To find the molar mass M, we use Avogadro's number NA=6.022×1023 mol−1:
M=m×NA
Substituting the values:
M=(1.1773×10−19)×(6.022×1023)
M≈7.09×104 g/mol
Final Answer
The molar mass of the plant virus is approximately 7.09×104 g/mol.
---
The virus is modeled as a cylinder. The volume V of a cylinder is given by the formula:
V=πr2h
Where:
- r is the radius of the cylinder
- h is the height (length) of the cylinder
- Diameter = 150 Å, so radius r=1502=75 Å
- Length h=5000 Å
- 1 Å=10−8 cm
- Radius r=75×10−8 cm
- Height h=5000×10−8 cm
V=π(75×10−8)2(5000×10−8)
V=π(5.625×10−15)(5.0×10−5)
V=π(2.8125×10−20) cm3
V≈8.83×10−20 cm3
Using the specific volume v=0.75 mL/g (which is equivalent to 0.75 cm3/g), we can find the mass m using the formula:
m=Vv
Substituting the values:
m=8.83×10−200.75
m≈1.1773×10−19 g
To find the molar mass M, we use Avogadro's number NA=6.022×1023 mol−1:
M=m×NA
Substituting the values:
M=(1.1773×10−19)×(6.022×1023)
M≈7.09×104 g/mol
The molar mass of the plant virus is approximately 7.09×104 g/mol.
Topper's Solved these Questions
- MOLE CONCEPTBOOK - ALLENCHAPTER - MOLE CONCEPTEXERCISE - Exercise - 04[B]
27 Videos
- MOLE CONCEPTBOOK - ALLENCHAPTER - MOLE CONCEPTEXERCISE - Exercise - 05(A)
21 Videos
- MOLE CONCEPTBOOK - ALLENCHAPTER - MOLE CONCEPTEXERCISE - Comprehension # 9
4 Videos
- IUPAC NOMENCLATUREBOOK - ALLENCHAPTER - IUPAC NOMENCLATUREEXERCISE - Exercise - 05(B)
7 Videos
- QUANTUM NUMBER & PERIODIC TABLEBOOK - ALLENCHAPTER - QUANTUM NUMBER & PERIODIC TABLEEXERCISE - J-ADVANCED EXERCISE
24 Videos
Similar Questions
A plant virus was found to consist of uniform cylindrical particles 100A in diameter and 4000A long The virus has a specific volume 0.314cm3g−1 If the virus particle is considered to be one molecule, what is its molecular weight ? .
View SolutionA plant virus contains spherical particles of radius 4Å. If the
density of virus is 12πgm/cm3, the molar mass of virus is -
View SolutionA mother cell disintegrate into sixty identical cells and each daughter cell further disintegrate into 24 smaller cells. The smallest cells are uniform cylindrical in shape with diameter of 120Å and each cell is 6000Å long. Determine molar mass of the mother cell if density of the smallest cell is 1.12g/cm3 :
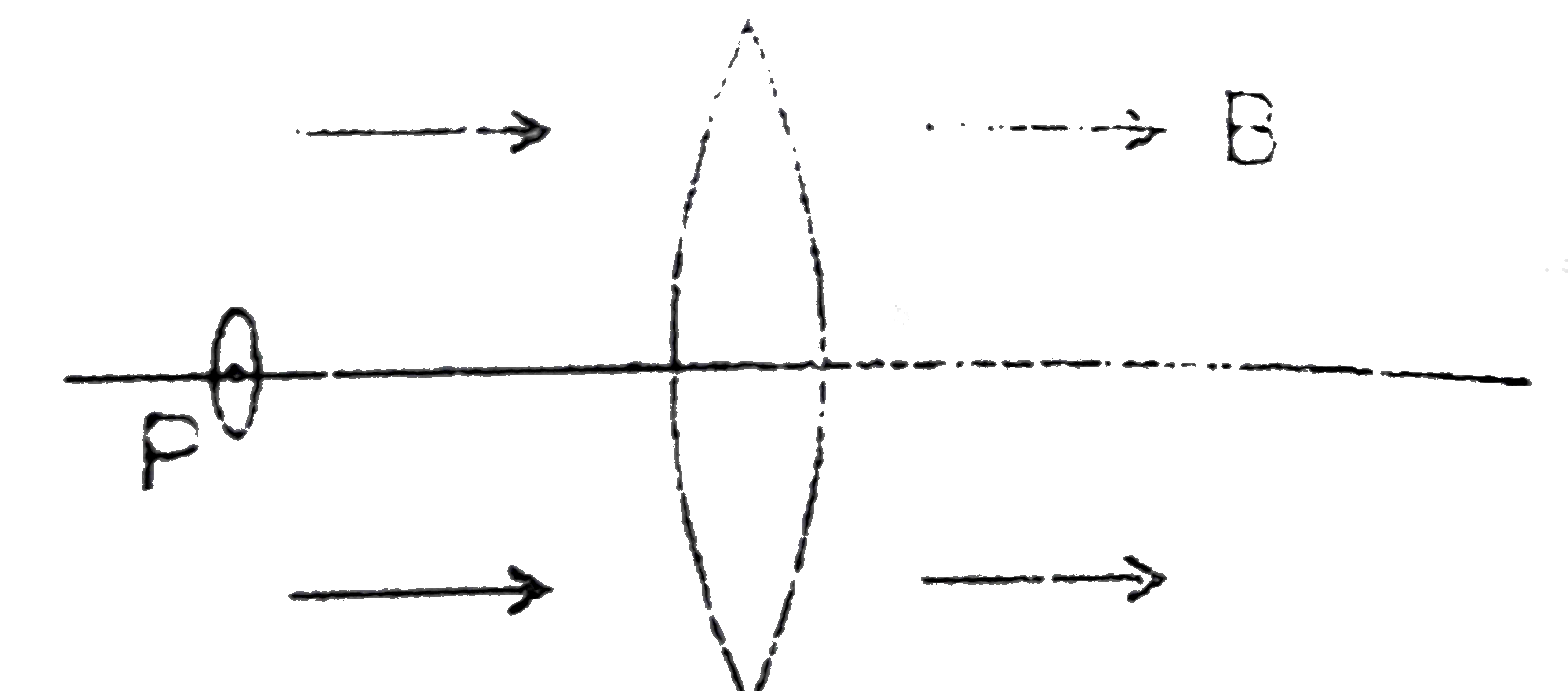
View SolutionFigure shows a convex lens of focal length 10cm lying in a uniform magnetic field B of magnitude 1.2T parallel to its principal axis.A particle havig a charge 2.0×10−3C and mass 2.0×10−5kg is projected perpendicular to the plane of the diagram with a speed of 4.8m/s.The particle moves along a circle with its centre on the principal axis at a distance of 15cm from the lens.The axis of the lens and of the circle are same.Show that the image of the particle goes along a circle and find the radius of that circle.
View SolutionA travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidal. The amplitude of vibration is 1.0cm and the displacement becomes zero 200 times per second. The linear mass density of the string is 0.10kgm−1 and it is kept under a tension of 90 N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0 the end x= 0 is at its positive extreme position. Write the wave equation. (c ) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10ms.
View SolutionThe word fluid means a substance having particles which readily of its magnitude (a small shear stress, which may appear to be of negligible will cause deformation in the fluid). Fluids are charactrised by such properties as density. Specific weight, specific gravity, viscosity etc. Density of a substance is defined as mass per unit volume and it is denoted by. The specific gravity represents a numerical ratio of two densities, and water is commonly taken as a reference substance. Specific gravity of a substance in written as the ratio of density of substance to the density of water. Specific weight represents the force exerted by gravity on a unit volume of fluid. It is related to the density as the product of density of a fluid and acceleration due to gravity. Viscosity is the most important and is recognized as the only single property which influences the fluid motion to a great extent. The viscosity is the property by virtue of which a fluid offers resistance to deformation under the influenece if shear force. The force between the layers opposing relative motion between them are known as forces of viscosity. When a boat moves slowly on the river remains at rest. Velocities of different layers are different. Let v be the velocity of the level at a distance y from the bed and V+dv be the velocity at a distance y+dy. The velocity differs by dv in going through a distance by perpendicular to it. The quantity dvdy is called velocity gradient. The force of viscosity between two layers of a fluid is proportional to velocity gradient and Area of the layer.
F∝A & F∝dvdy
F=−ηAdvdy (−ve sign shown the force is frictional in nature and opposes relative motion. η coefficient of dynamic viscosity
Shear stress FA=−ηdvdy
and simultaneously kinematic viscosity is defined as the dynamic viscosity divided by the density. If is denoted as v. The viscosity of a fluid depends upon its intermolecular structure. In gases, the molecules are widely spaced resulting in a negligible intermolecular cohesion, while in liquids the molecules being very close to each other, the cohesion is much larger with the increases of temperature, the cohesive force decreases rapidly resulting in the decreases of viscosity. In case of gases, the viscosity is mainly due to transfer of molecular momentum in the transerve direction brought about by the molecular agitation. Molecular agitation increases with rise in temperature. Thus we conclude that viscosity of a fluid may thus be considered to be composed of two parts, first due to intermolecuar cohesion and second due to transfer of molecular momentum.
If the velocity profile is given by
v=23y−y2v is velocity in m/secy is in meter above the bad. Determine shear stress at y=0.15m, & η=0.863Ns/m2
View SolutionA particle having a charge20μC and mass 20μg moves along a circle of radius 5.0 cm under the action of a magnetic field 5.0 cm under the action of a magnetic field B = 1.0 T. When the particle is at a point P, a uniform electric field is switched on and it is found that the particla continues on the tangent through P qith a uniform velocity. Find the electric field.
View SolutionThe word fluid means a substance having particles which readily of its magnitude (a small shear stress, which may appear to be of negligible will cause deformation in the fluid). Fluids are charactrised by such properties as density. Specific weight, specific gravity, viscosity etc. Density of a substance is defined as mass per unit volume and it is denoted by. The specific gravity represents a numerical ratio of two densities, and water is commonly taken as a reference substance. Specific gravity of a substance in written as the ratio of density of substance to the density of water. Specific weight represents the force exerted by gravity on a unit volume of fluid. It is related to the density as the product of density of a fluid and acceleration due to gravity. Viscosity is the most important and is recognized as the only single property which influences the fluid motion to a great extent. The viscosity is the property by virtue of which a fluid offers resistance to deformation under the influenece if shear force. The force between the layers opposing relative motion between them are known as forces of viscosity. When a boat moves slowly on the river remains at rest. Velocities of different layers are different. Let v be the velocity of the level at a distance y from the bed and V+dv be the velocity at a distance y+dy. The velocity differs by dv in going through a distance by perpendicular to it. The quantity dvdy is called velocity gradient. The force of viscosity between two layers of a fluid is proportional to velocity gradient and Area of the layer.
F∝A & F∝dvdy
F=−ηAdvdy (−ve sign shown the force is frictional in nature and opposes relative motion. η coefficient of dynamic viscosity
Shear stress FA=−ηdvdy
and simultaneously kinematic viscosity is defined as the dynamic viscosity divided by the density. If is denoted as v. The viscosity of a fluid depends upon its intermolecular structure. In gases, the molecules are widely spaced resulting in a negligible intermolecular cohesion, while in liquids the molecules being very close to each other, the cohesion is much larger with the increases of temperature, the cohesive force decreases rapidly resulting in the decreases of viscosity. In case of gases, the viscosity is mainly due to transfer of molecular momentum in the transerve direction brought about by the molecular agitation. Molecular agitation increases with rise in temperature. Thus we conclude that viscosity of a fluid may thus be considered to be composed of two parts, first due to intermolecuar cohesion and second due to transfer of molecular momentum.
Viscosity of liquids
View SolutionSpecific volume of cylindrical virus particle is 6.02×10−2cc/g whose radius and length 7Å and 10Å respectively. If NA=6.02×1023, find molecular weight of virus:
View SolutionA particle having charge of 20μC and mass 20μg moves along as circle of radius 5cm under the action of a magnetif field B=0.1 tesla. When the particle is at P, uniform transverse electric field is switched on an it is found that the particle continues along the tangent with a uniform velocity. Find the electric field

View Solution
