Question

State and explain Kirchhoff's laws.

Explanation

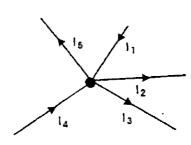
Kirchhoff.s First law: It states that algebraic sum of currents meeting at a point in an electrical circuit is zero. It is also called junction rule. Explanation: Consider a point O in an electrical circuit at which currents `I_(1), I_(2), I_(3), I_(4) and I_(5)` are flowing through the five conductors in the directions as shown in Fig. below. Let us adopt the following convention: The current flowing in a conductor towards the point O is taken as positive and the current flowing away from the point O is taken as negative. Likewise, currents `I_(1) and I_(4)` flowing towards the point O are positive, while the currents `I_(2), I_(3) and I_(5)` are negative. Therefore, according to Kirchhoff.s First Law,
`I_(1) + (-I_(2)) + (-I_(3)) + I_(4) + (-I_(5))= 0`
or `I_(1)- I_(2)- I_(3) + I_(4) - I_(5)= 0`

Kirchhoff.s second law: It states that in any closed part of an electrical circuit, the algebraic sum of the e.m.f.s is equal to the algebraic sum of the products of the resistances and currents flowing through them. It is also called loop rule.
Sign Convention :
1. If the path taken to traverse the resistance is along the direction of current, then the product of current and resistance is taken as negative i.e., -IR.
2. If the path taken to traverse the resistance is against the direction of current, then product of current and resistance is taken as positive i.e., + IR

3. If the electric current flows through the cell from its negative to positive terminal then emf of cell is taken as positive (+E).
4. If the electric current flows through the cell from its positive to negative terminal then emf of the cell is taken as negative (-E)

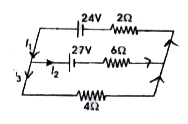
To understand these rules we consider the following electrical circuit. Applying loop law to the upper and lower loops anticlockwise,
`-2I_(1)- 6I_(2) + 24-27=0`
or `-2I_(1)-6I_(2)=3`....(i)
and `-4 I_(3) + 6I_(2)= -27`
or `-4 (I_(1)- I_(2)) + 6I_(2)= -27 (because I_(1)= I_(2) + I_(3) or I_(3)= I_(1)- I_(2))`
or `-4I_(1) + 4I_(2) + 6I_(2)= -27`
or `-4I_(1) + 10I_(2)= -27` ...(ii)
Solving (i) and (ii), we get `I_(1)= 3A, I_(2)= -1.5A`
`therefore I_(3)= I_(1)- I_(2)= 3-(-1.5)`
= 4.5A