Explain the principle of Wheatstone bridge for determining and unknown resistance. How is it realised in actual practice in the laboratory?Solution in Punjabi
Wheatstone bridge : Wheatstone bridge consists of four resistances P, Q, R and S arranged so as to form a quadrilateral ABCD as shown in fig. A cell E and a key K are connected between points A and C. A galvanometer G and a tapping key are connected between points B and D. On closing the key K first and then key , if galvanometer shows no deflection, then bridge is said to be balanced. In that case, and
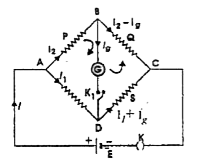
Knowing P, Q and R, we can calculate unknown resistance S.
Proof Let E= emf of the cell
I = Total current given by the cell.
At junction A, current I is divided into two parts, (flowing through arm (AD) and (flowing through arm AB). At junction B, current is again divided into two parts (through BD) and (through BC). At D, current combine and hence current flowing through DC is . At C, current combine and flows out and completes the circuit. Using Kirchhoff.s Second law in closed mesh ABDA.
...(I)
where G= Resistance of galvanometer
Using Kirchhoff.s second law in closed circuit BDCB, ...(II)
When bridge is balanced, i.e., when no current flows through the galvanometer (this can be done by adjusting the value of resistance R), then
Putting , in eqns (I) and (II) we get
or ...(III)
and
...(IV)
Dividing (III) by (IV),
Hence the proof.
Topper's Solved these Questions
- ELECTRICAL MEASUREMENTSBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRICAL MEASUREMENTSEXERCISE - Long Answer Type Questions
7 Videos
- ELECTRICAL MEASUREMENTSBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRICAL MEASUREMENTSEXERCISE - Numericals Problems
9 Videos
- ELECTRICAL MEASUREMENTSBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRICAL MEASUREMENTSEXERCISE - Most Expected Questions
7 Videos
- ELECTRICAL DEVICESBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRICAL DEVICESEXERCISE - (MOST EXPECTED QUESTIONS 2 MARK)
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - NUMERICAL PROBLEMS
26 Videos
Similar Questions
State and explain Kirchhoff's laws.
View SolutionA cell of e.m.f. 1 V gives a balance point at 40 cm length of a potentioeter wire. For another cell, the balance point shifts to 60 cm. Find the e.m.f. of the second cell.
View SolutionWhy is a slide wire bridge also called a metre bridge?
View SolutionWhy the core of a transformer made of a magnetic material of high permeability?
View SolutionA magnetic field of 2×10−2T acts at right angles to a coil of area 100cm2 with 50 turns. The average e.m.f. induced in the coil is 0.1 V, When it is removed form the field in the time t. The value of t is
View SolutionExplain the determination of unknown resistance using meter bridge.
View Solutionकिरचॉफ के नियमो को लिखिए तथा उसके आधार पर व्हीटस्टोन सेतु का सिद्धांत समझाइए ।
View Solutionव्हीटस्टोन ब्रिज द्वारा प्रतिरोध को नापने में ज्ञात तथा अज्ञात प्रतिरोधों को उत्क्रमित किया जाता है,जिसका निराकरण करने के लिए वह है -
View SolutionHow resistance can be determined using the principle of Wheatstone bridge ? Derive the principle .
View SolutionExplain the determination of unknown resistance using meter bridge.
View Solutionव्हीटस्टोन सेतु द्वारा एक प्रतिरोध के मापन में ज्ञात तथा अज्ञात प्रतिरोध को आपस में बदला जाता………...है, को उदासीन करने के लिए।
View Solutionदिए गए चित्र में यदि व्हीटस्टोन सेतु संतुलित है, तो अज्ञात प्रतिरोध X का मान ज्ञात कीजिए |
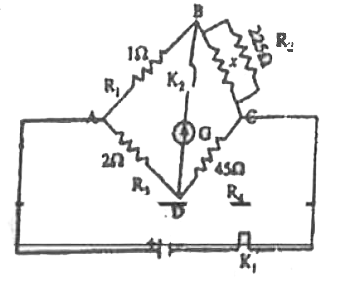
View SolutionExplain the determination of unknown resistance using meter bridge.
View SolutionDraw the circuit diagram for wheatstone bridge to determine unknown resistance. Write condition for balancing of the bridge.
View SolutionExplain the principle of working of a meter bridge. Draw the circuit diagram for determination of an unknown resistance using it.
View SolutionWhat is the principle of Wheatstone bridge for determining an unknown resistance ? How is it realised in actual practice in the laboratory?
View Solution
