एक फर्म A और B दो प्रकार के उत्पाद बनाती है और उन्हें क्रमशः प्रति इकाई ₹6 तथा ₹ 3 के लाभ पर बेचती है। प्रत्येक उत्पाद दो मशीनों M1 और M2 से गुजरता है। A उत्पाद को M1 और M2 पर क्रमश: 1 मिनट और 2 मिनट लगते हैं जबकि B उत्पाद को M1 और M2 पर क्रमश: 1 मिनट और 1 मिनट लगते हैं। मशीन M1 और M2 प्रति दिवस क्रमशः 5 घण्टे तथा 6 घण्टे के लिए उपलब्ध है। अधिकतम लाभ के लिए फर्म को प्रतिदिन दोनों प्रकारों की कितनी संख्या उत्पादित करना चाहिए। ग्राफीय विधि से हल कीजिए।
The correct Answer is:Rs. 1,020
Step by step video, text & image solution for एक फर्म A और B दो प्रकार के उत्पाद बनाती है और उन्हें क्रमशः प्रति इकाई ₹6 तथा ₹ 3 के लाभ पर बेचती है। प्रत्येक उत्पाद दो मशीनों M_(1) और M_(2) से गुजरता है। A उत्पाद को M_(1) और M_(2) पर क्रमश: 1 मिनट और 2 मिनट लगते हैं जबकि B उत्पाद को M_(1) और M_(2) पर क्रमश: 1 मिनट और 1 मिनट लगते हैं। मशीन M_(1) और M_(2) प्रति दिवस क्रमशः 5 घण्टे तथा 6 घण्टे के लिए उपलब्ध है। अधिकतम लाभ के लिए फर्म को प्रतिदिन दोनों प्रकारों की कितनी संख्या उत्पादित करना चाहिए। ग्राफीय विधि से हल कीजिए। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- रैखिक प्रोग्रामन BOOK - SBPD PUBLICATIONCHAPTER - रैखिक प्रोग्रामन EXERCISE - अभ्यास 12.2 (परिवहन सम्बन्धी समस्या (Transportation Problems) )
5 Videos
- रैखिक प्रोग्रामन BOOK - SBPD PUBLICATIONCHAPTER - रैखिक प्रोग्रामन EXERCISE - अभ्यास 12.2 (विविध समस्याएँ (Miscellaneous Problems) )
10 Videos
- रैखिक प्रोग्रामन BOOK - SBPD PUBLICATIONCHAPTER - रैखिक प्रोग्रामन EXERCISE - अभ्यास 12.1
13 Videos
- यादृच्छिक चर तथा प्रायिकता बंटनBOOK - SBPD PUBLICATIONCHAPTER - यादृच्छिक चर तथा प्रायिकता बंटनEXERCISE - कम्पटीशन कॉर्नर
3 Videos
- रैखिक समीकरणों के निकाय का हल BOOK - SBPD PUBLICATIONCHAPTER - रैखिक समीकरणों के निकाय का हल EXERCISE - कम्प्टीशन कॉर्नर
2 Videos
Similar Questions
एक एयरलाइन किसी समूह को प्लेन चार्टर करने हेतु सहमत है। समूह को 100 प्रथम श्रेणी सीट, 300 टूरिस्ट श्रेणी सीट की आवश्यकता है। एयरलाइन दो प्रकार के मॉडल का प्रयोग करता है, 314 प्लेन जिसमें 20 प्रथम श्रेणी और 30 टूरिस्ट श्रेणी की सीट है तथा 535 प्लेन जिसमें 20 प्रथम श्रेणी और 60 टूरिस्ट श्रेणी की सीट उपलब्ध हैं। 314 प्लेन की प्रत्येक उड़ान पर लागत ₹1 लाख तथा 535 प्लेन की प्रत्येक उड़ान पर ₹ 1.5 लाख है। उड़ान पर कम-से-कम लागत आये, इस हेतु प्रत्येक प्रकार के कितने प्लेन का उपयोग करना चाहिए ? रैखिक प्रोग्रामन का सूत्रीकरण कीजिए।
View Solutionअमित के गणित के शिक्षक ने उसे सवालों की तीन लम्बी सूची दी इस शर्त के साथ कि उनमें से 100 से अधिक (सही हल) नहीं जमा करना है। प्रथम सेट का प्रत्येक सवाल 5 अंक का है, द्वितीय सेट का 4 अंक, तृतीय सेट का 6 अंक। अमित को 5 अंक के सवालों को हल करने में 3 मिनट लगते हैं, जबकि 4 अंक वालों पर 2 मिनट, 6 अंक वालों पर 4 मिनट। चूँकि वह अन्य विषयों का भी अध्ययन करता है अत: वह गणित पर 312 घण्टे से अधिक समय नहीं दे सकता है। प्रथम दो सेट पर वह 212 घण्टे से अधिक समय नहीं दे सकता है। अधिकतम अंक प्राप्त करने हेतु रैखिक प्रोग्रामन का सूत्रीकरण कीजिए।
View Solutionआलेखीय विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए
निम्न व्यवरोधों के अंतर्गत Z = 20x + 10y का न्यूनतमीकरण कीजिए
x+2y≤40,3x+y≥30,4x+3y≥60 तथा x,y≥0
View Solutionयदि समुच्चय {0, 1, 2, 3, ......., 10} में से दो विभिन्न संख्याएँ निकाली गईं तो उनके योगफल तथा उनके अन्तर के निरपेक्ष मान, दोनों के चार के गुणांक होने की प्रायिकता है
View Solutionवास्तविक संख्या α के लिए यदि रैखिक समीकरण निकाय ⎡⎢⎣1αα2α1αα2α1⎤⎥⎦⎡⎢⎣xyz⎤⎥⎦=⎡⎢⎣1−11⎤⎥⎦ के अनन्त हल है तब 1+α+α2=
View SolutionThe lines y=m1x,y=m2xandy=m3x make equal intercepts on the line x+y=1. Then (a) 2(1+m1)(1+m3)=(1+m2)(2+m1+m3) (b)(1+m1)(1+m3)=(1+m2)(1+m1+m3) (c)(1+m1)(1+m2)=(1+m3)(2+m1+m3) (d)2(1+m1)(1+m3)=(1+m2)(1+m1+m3)
View Solutionमाना दो समीकरणें ax2+2hxy+by2=0 तथा y2−(m1+m2)xy+m1m2x2=0 एक ही वक्र को निरूपित करती है तो सिद्ध कीजिए m1+m2=−2hb तथा m1m2=ab
View Solutionसूत्र (m1x2+m2x1m1+m2,m1y2+m2y1m1+m2) क्या कहलाता है ?
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View SolutionIf (m1,1/m1),i=1,2,3,4 are concyclic points, then the value of m1m2m3m4 is
View Solutionm1 व m2 द्रव्यमानों के दो कणों के किसी निकाय का द्रव्यमान केन्द्र, m1 से d1 दूरी पर तथा m2 से d2 दूरी पर इस प्रकार से है कि
View SolutionProve that the orthocentre of the triangle formed by the three lines
y=m1x+a/m1,y=m2x+a/m2, and y=m3x+a/m3 is
{−a,a(1m1+1m2+1m3+1m1m2m3)}
View SolutionIf m_(1)और m_(2) ellipsoid (x^(2))/(16)+(y^(2))/(9)=1 are the slopes of the tangents of the line passing through (5, 4), then (m_(1)+m_(2))-(m_(1)m_(2)) is equal to
View Solution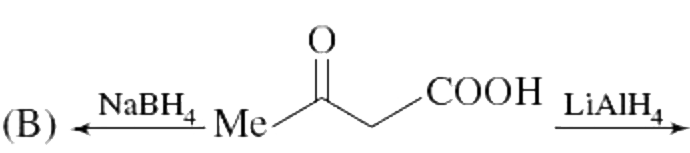 (A)
(A)
a और B क्रमश है :
View Solutionअभिक्रियाओं के निम्नलिखित अनुक्रम पर विचार कीजिए: मध्यवर्ती उत्पाद (X) और (Y) क्रमशः हैं:
View SolutionM_(1)=56 वाली गैस 1 के T_(1) और M_(2) = 44 वाली गैस 2 के T_(2) के मध्य क्या संबंध होगा, यदि गैस 1 की औसत चाल, गैस 2 की अति संभाव्य गति के बराबर है?
View Solution
