A shot is fired at an angle α to the horizontal up a hill of inclination β to the horizontal. Then it strikes the hill horizontally if
tanα=2tanβ
tanα=tanβ
tanα.tanβ=1
None
The correct Answer is:A
To solve the problem of determining the condition under which a shot fired at an angle α to the horizontal strikes a hill inclined at an angle β horizontally, we can follow these steps:
Step 1: Understand the Geometry of the Problem
- We have a projectile launched at an angle α with respect to the horizontal.
- The hill is inclined at an angle β to the horizontal.
- When the projectile strikes the hill, it does so horizontally, meaning its vertical component of velocity at that point is zero.
Step 2: Analyze the Components of Motion
- The initial velocity u can be broken down into its horizontal and vertical components:
- Horizontal component: ux=ucosα
- Vertical component: uy=usinα
Step 3: Determine the Condition for Horizontal Strike
- When the projectile strikes the hill horizontally, the vertical component of the velocity at the point of impact must be zero.
- The vertical motion can be described by the equation:
vy=uy−gt
where g is the acceleration due to gravity and t is the time of flight.
- Setting vy=0 gives:
0=usinα−gt⟹t=usinαg
Step 4: Calculate the Time of Flight to the Hill
- The time of flight until it strikes the hill can also be expressed in terms of the incline. The projectile travels a horizontal distance x and a vertical distance y until it reaches the hill.
- The vertical displacement of the projectile when it strikes the incline can be expressed in terms of the angle β:
y=xtanβ
Step 5: Relate the Horizontal and Vertical Displacements
- The horizontal distance traveled in time t is:
x=ucosα⋅t=ucosα⋅usinαg=u2sinαcosαg
- The vertical displacement at the same time is:
y=usinα⋅t−12gt2=usinα⋅usinαg−12g(usinαg)2
Simplifying gives:
y=u2sin2αg−12u2sin2αg=u2sin2α2g
Step 6: Set the Vertical Displacement Equal to the Hill's Height
- Setting the vertical displacement equal to the height of the incline:
u2sin2α2g=(u2sinαcosβg)tanβ
Rearranging gives:
sin2α=2sinαcosβtanβ
Step 7: Simplify to Find the Relation Between Angles
- This leads to the relation:
tanα=2tanβ
Final Conclusion
Thus, the condition for the projectile to strike the hill horizontally is:
tanα=2tanβ
- We have a projectile launched at an angle α with respect to the horizontal.
- The hill is inclined at an angle β to the horizontal.
- When the projectile strikes the hill, it does so horizontally, meaning its vertical component of velocity at that point is zero.
- The initial velocity u can be broken down into its horizontal and vertical components:
- Horizontal component: ux=ucosα
- Vertical component: uy=usinα
- When the projectile strikes the hill horizontally, the vertical component of the velocity at the point of impact must be zero.
- The vertical motion can be described by the equation:
vy=uy−gt
where g is the acceleration due to gravity and t is the time of flight.
0=usinα−gt⟹t=usinαg
- The time of flight until it strikes the hill can also be expressed in terms of the incline. The projectile travels a horizontal distance x and a vertical distance y until it reaches the hill.
- The vertical displacement of the projectile when it strikes the incline can be expressed in terms of the angle β:
y=xtanβ
- The horizontal distance traveled in time t is:
x=ucosα⋅t=ucosα⋅usinαg=u2sinαcosαg
y=usinα⋅t−12gt2=usinα⋅usinαg−12g(usinαg)2
Simplifying gives:
y=u2sin2αg−12u2sin2αg=u2sin2α2g
- Setting the vertical displacement equal to the height of the incline:
u2sin2α2g=(u2sinαcosβg)tanβ
Rearranging gives:
sin2α=2sinαcosβtanβ
- This leads to the relation:
tanα=2tanβ
Thus, the condition for the projectile to strike the hill horizontally is:
tanα=2tanβ
Similar Questions
Consider an object P on an inclined plane of inclination β.
A shot is fired O at an angle α with horizontal. Find the relation between α and β, if the shot hits the object horizontally.

View SolutionA particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View Solution
Knowledge Check
The angle of inclination with the horizontal is
Aangle of bankingBbanking angleCangle of contactDboth 'a' and 'b'A trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.
 AEqual to αBGreater than αCEqual to α2DLesser than α
AEqual to αBGreater than αCEqual to α2DLesser than αA projectile is thrown upward with a velocity v0 at an angle α to the horizontal. The change in velocity of the projectile when it strikes the same horizontal plane is
Av0sinα vertically downwardB2v0sinα vertically downwardC2v0sinα vertically upwardDzero
A trolley containing a liquid slides down a smooth inclined plane of angle α with the horizontal. Find the angle of inclination θ of the free surface with the horizontal.

View SolutionA uniform rod of length L is placed with one end in contact with the horizontal and is then inclined at an angle α to the horizontal and allowed to fall without slipping at contact point. When it becomes horizontal, its angular velocity will be
View SolutionA shot is fired at an angle θ to the horizontal such that it strikes the hill while moving horizontally. Find the initial angle of projection θ.
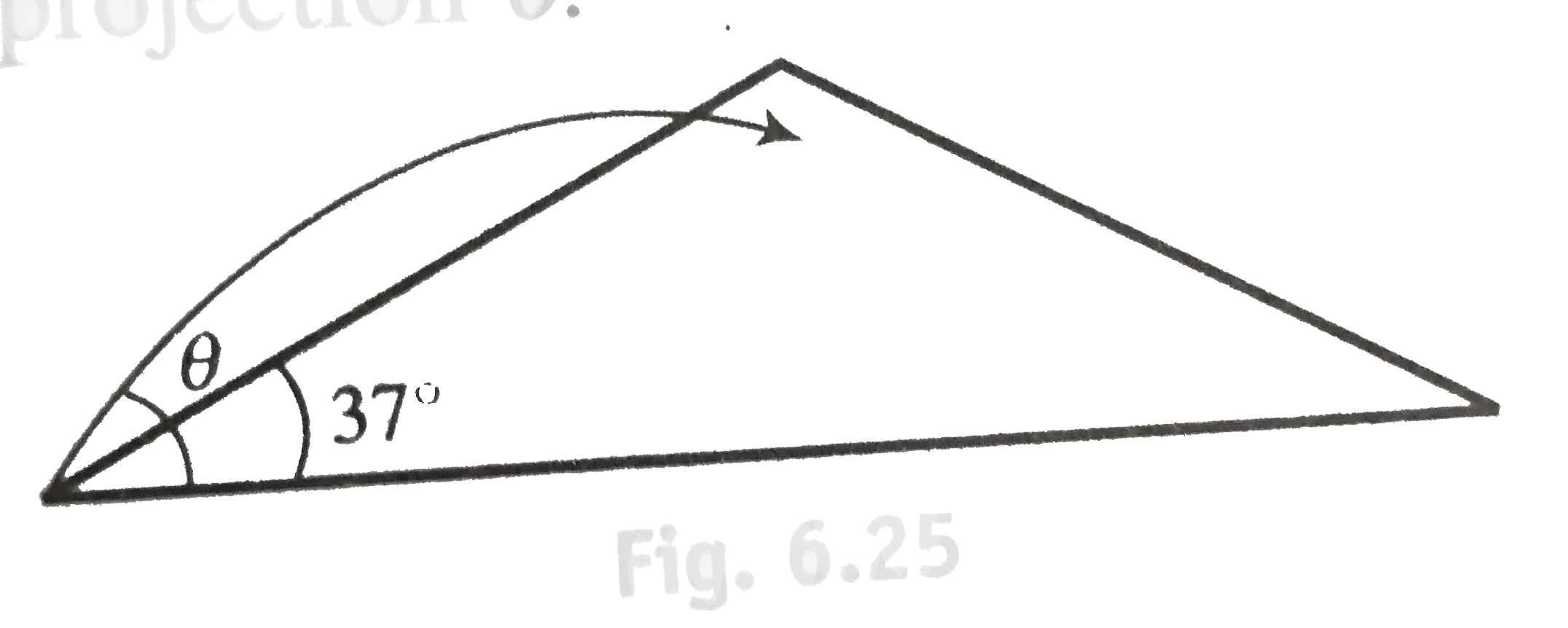
View SolutionA particle is projected at an angle α with the horizontal from the foot of an inclined plane making an angle β with horizontal . Which of the following expressions holds good if the particle strikes the inclined plane normally?
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View Solution
