The velocity and direction of projection of a shot which passes in horizontal direction just over the top of a wall which is 50 yds. away and 75 feet high.
40,30∘
40√6,45∘
50,60∘
None
The correct Answer is:B
To solve the problem of finding the velocity and direction of projection of a shot that passes just over the top of a wall, we will follow these steps:
Step 1: Understand the Problem
We need to find the initial velocity (U) and the angle of projection (α) for a projectile that just clears a wall that is 75 feet high and located 50 yards away.
Step 2: Convert Units
Since the height is given in feet and the distance in yards, we need to convert everything to the same unit.
1 yard = 3 feet, so:
- Distance to the wall = 50 yards = 50 × 3 = 150 feet.
- Height of the wall = 75 feet.
Step 3: Use the Maximum Height Formula
The maximum height (H) reached by a projectile is given by the formula:
H=U2sin2α2g
Where:
- g = acceleration due to gravity = 32 ft/s² (approximately).
Substituting the values we have:
75=U2sin2α2×32
This simplifies to:
U2sin2α=75×64
U2sin2α=4800 (Equation 1)
Step 4: Use the Range Formula
The range (R) of a projectile is given by:
R=U2sin2αg
Since the range to the wall is 150 feet, we can write:
150=U2sin2α32
Using the identity sin2α=2sinαcosα, we get:
150=U2(2sinαcosα)32
This simplifies to:
U2sin2α=150×32
U2sin2α=4800 (Equation 2)
Step 5: Relate the Two Equations
From Equation 1 and Equation 2, we have:
U2sin2α=U2sin2α
This implies:
sin2α=sin2α
Using the identity sin2α=2sinαcosα:
sin2α=2sinαcosα
Dividing both sides by sinα (assuming sinα≠0):
sinα=2cosα
This gives:
tanα=2
Step 6: Find the Angle of Projection
From tanα=2, we can find α:
α=tan−1(2)
Calculating this gives approximately α≈63.43∘.
Step 7: Calculate the Initial Velocity
Now substituting sinα and cosα back into Equation 1 to find U:
Using sinα=2√5 and cosα=1√5:
U2(2√5)2=4800
U2⋅45=4800
U2=4800⋅54
U2=6000
U=√6000=10√60
Final Answer
The initial velocity U is 10√60 feet per second, and the angle of projection α is approximately 63.43∘.
We need to find the initial velocity (U) and the angle of projection (α) for a projectile that just clears a wall that is 75 feet high and located 50 yards away.
Since the height is given in feet and the distance in yards, we need to convert everything to the same unit.
1 yard = 3 feet, so:
- Distance to the wall = 50 yards = 50 × 3 = 150 feet.
- Height of the wall = 75 feet.
The maximum height (H) reached by a projectile is given by the formula:
H=U2sin2α2g
Where:
- g = acceleration due to gravity = 32 ft/s² (approximately).
75=U2sin2α2×32
This simplifies to:
U2sin2α=75×64
U2sin2α=4800 (Equation 1)
The range (R) of a projectile is given by:
R=U2sin2αg
Since the range to the wall is 150 feet, we can write:
150=U2sin2α32
Using the identity sin2α=2sinαcosα, we get:
150=U2(2sinαcosα)32
This simplifies to:
U2sin2α=150×32
U2sin2α=4800 (Equation 2)
From Equation 1 and Equation 2, we have:
U2sin2α=U2sin2α
This implies:
sin2α=sin2α
Using the identity sin2α=2sinαcosα:
sin2α=2sinαcosα
Dividing both sides by sinα (assuming sinα≠0):
sinα=2cosα
This gives:
tanα=2
From tanα=2, we can find α:
α=tan−1(2)
Calculating this gives approximately α≈63.43∘.
Now substituting sinα and cosα back into Equation 1 to find U:
Using sinα=2√5 and cosα=1√5:
U2(2√5)2=4800
U2⋅45=4800
U2=4800⋅54
U2=6000
U=√6000=10√60
The initial velocity U is 10√60 feet per second, and the angle of projection α is approximately 63.43∘.
Similar Questions
Knowledge Check
At which place direction of earth's magnetic field is horizontal ?
AMagnetic pole.BGeographic poleCMagnetic meridian.DMagnetic equator.A body is projected with velocity u at an angle of projection θ with the horizontal. The direction of velocity of the body makes angle 30∘ with the horizontal at t=2s and then after 1s it reaches the maximum height. Then
Au=20√3ms−1,Bθ=60∘Cθ=30∘Du=10√3ms−1A shell fired from the ground is just able to cross in a horizontal direction the top of a wall 90m away and 45m high. The direction of projection of the shell will be:
A25∘B30∘C45∘Dnone of these
A motor boat, with its engine on in a running river and blow n over by a horizontal wind is observed to travelat 20 kph in a direction 53∘ East of North. The velocity of the boat with its engine on in still water & blown over by the horizontal wind is 4kph East ward and the velocity of the boat with its engine on over the running river, in the absence of wind is 8 kph due south. Find:
(a) The velocity of the boat in magnitude and direction, over still water in the absence of wind.
(b) The velocity of the wind in magnitude and direction.
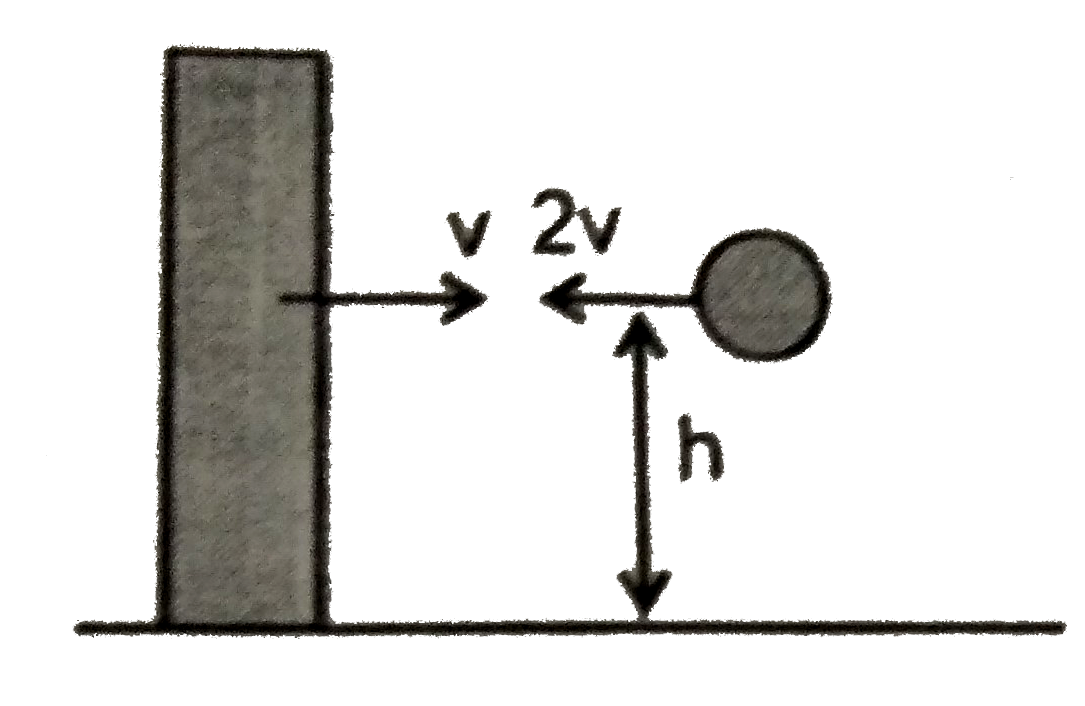
View SolutionA ball collides elastically with a massive wall moving towards it with a velocity of v as shown. The collision occurs at a height of h above ground level and the velocity of the ball just before collision is 2v in horizontal direction. The distance between the foot of the wall and the point on the ground where the ball lands, at the instant the ball lands, will be :
View SolutionA projectile is thrown in the upward direction making an angle of 60∘ with the horizontal direction with a velocity of 147ms−1 then the time after which its inclination with the horizontal is 45∘, is :
View SolutionA projectile is thrown in the upward direction making an angle of 60∘ with the horizontal direction with a velocity of 147ms−1 then the time after which its inclination with the horizontal is 45∘, is :
View SolutionA shot is fired from a point at a distance of 200m from the foot of a tower 100m high so that it just passes over it horizontally. The direction of shot with horizontal is.
View Solution
