Let PQandRS be tangent at the extremities of the diameter PR of a circle of radius r. If PSandRQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQxRS .
√PQ.RS
PQ+RS2
2PQ.RSPQ+RS
√PQ2+RS22
The correct Answer is:A
Step by step video, text & image solution for Let P Qa n dR S be tangent at the extremities of the diameter P R of a circle of radius rdot If P Sa n dR Q intersect at a point X on the circumference of the circle, then prove that 2r=sqrt(P Q x R S) . by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THE CIRCLE BOOK - ML KHANNACHAPTER - THE CIRCLE EXERCISE - Problem Set (1) (TRUE AND FALSE)
3 Videos
- THE CIRCLE BOOK - ML KHANNACHAPTER - THE CIRCLE EXERCISE - Problem Set (1) (FILL IN THE BLANKS)
10 Videos
- TANGENTS AND NORMALSBOOK - ML KHANNACHAPTER - TANGENTS AND NORMALSEXERCISE - SELF ASSESSMENT TEST (MULTIPLE CHOICE QUESTIONS)
19 Videos
- THE ELLIPSEBOOK - ML KHANNACHAPTER - THE ELLIPSEEXERCISE - SELF ASSESSMENT TEST
9 Videos
Similar Questions
Let PQ and RS be tangent at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQ×RS .
View SolutionLet PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals
View Solution
Knowledge Check
Let PQandRS be tangent at the extremities of the diameter PR of a circle of radius r. If PSandRQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQxRS .
A√PQ.RSBPQ+RS2C2PQ.RSPQ+RSD√PQ2+RS22The tangents are drawn at the extremities of diameter AB of a circle with centre P. If a tangent to the circle at the point C Intersects the other two tangents at Q and R, then the measure of the ∠QPR is
A45∘B60∘C90∘D180∘Tangents to a circle at points P and Q on the circle intersect at a point R. If PQ= 6 and PR= 5 then the radius of the circle is
A133B4C154D165
Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. PS and RQ intersect at a point X on the circumference of the circle. If PQ = 9 and RS = 4, then the diameter of the circle is :
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
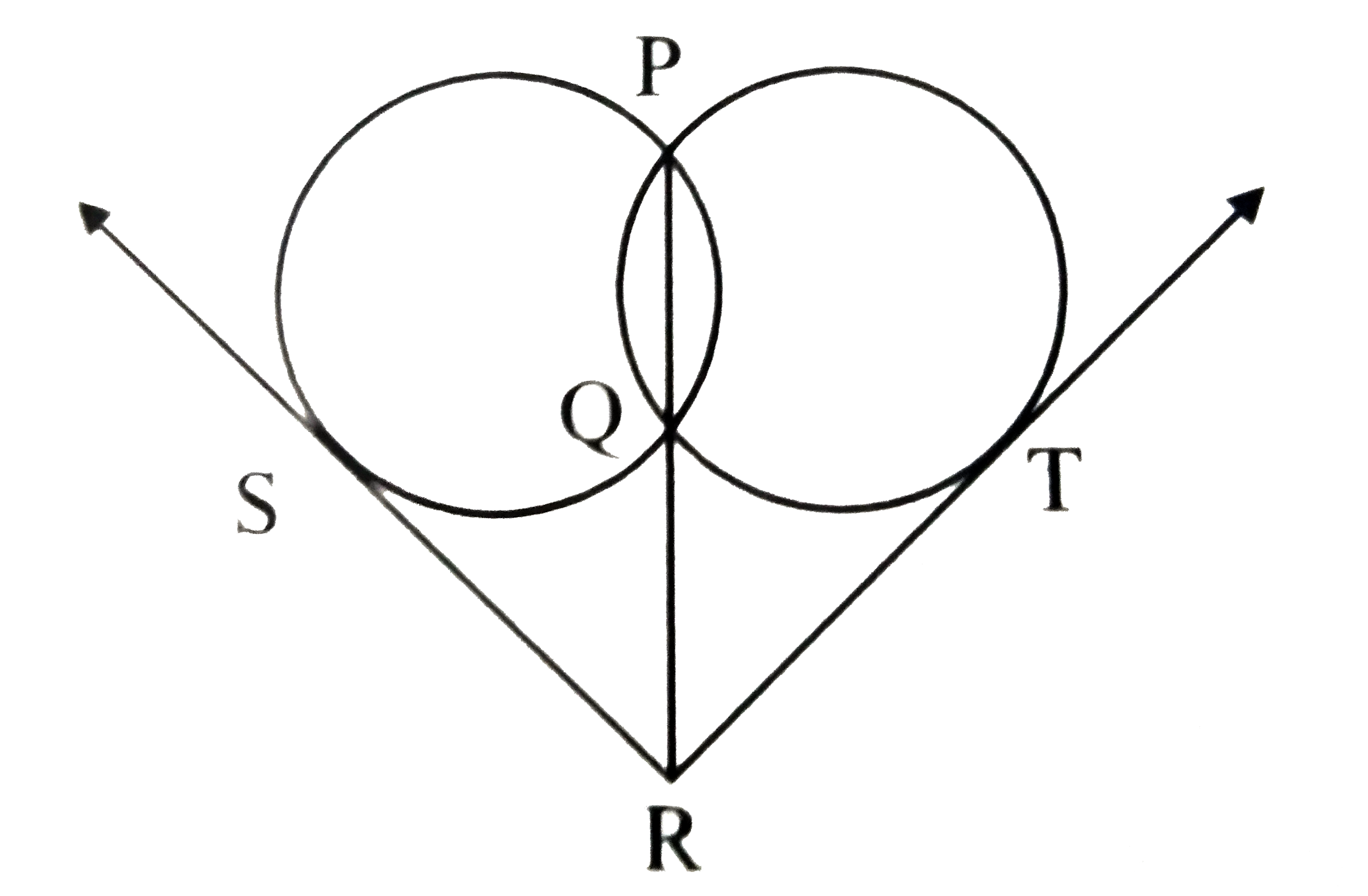
View SolutionP, Q,S and R are points on the circumference of a circle of radius r, such that POR is an equilateral triangle and PS is a diameter of the circle. What is the perimeter of the quadrilateral PQSR?
View SolutionP, Q, R and S are the points on the circumference of a circle of radius r, such that PQR is an equilateral triangle and PS is a diameter of circle. What is the perimeter of the quadrilateral PQSR?
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View Solution
