Three cloth merchants have total length of cloth in 57 meters, 69 meters and 93 meters. Find the greatest measure (meter) which can measure the clothes completely (exactly)
6
1
7
None
The correct Answer is:D
To find the greatest measure (in meters) that can measure the lengths of cloth (57 meters, 69 meters, and 93 meters) completely, we need to determine the Highest Common Factor (HCF) of these three lengths. Here’s a step-by-step solution:
Step 1: List the lengths of cloth
The lengths of cloth are:
- Cloth 1: 57 meters
- Cloth 2: 69 meters
- Cloth 3: 93 meters
Step 2: Find the prime factorization of each length
1. Prime Factorization of 57:
- 57 can be divided by 3 (57 ÷ 3 = 19).
- Therefore, the prime factorization of 57 is:
57=3×19
2. Prime Factorization of 69:
- 69 can also be divided by 3 (69 ÷ 3 = 23).
- Therefore, the prime factorization of 69 is:
69=3×23
3. Prime Factorization of 93:
- 93 can again be divided by 3 (93 ÷ 3 = 31).
- Therefore, the prime factorization of 93 is:
93=3×31
Step 3: Identify the common factors
From the prime factorizations:
- 57 = 3 × 19
- 69 = 3 × 23
- 93 = 3 × 31
The only common prime factor among all three numbers is 3.
Step 4: Determine the HCF
Since 3 is the only common factor, the HCF of 57, 69, and 93 is:
HCF=3
Step 5: Conclusion
The greatest measure (in meters) that can measure the lengths of cloth completely is:
Answer=3 meters
---
The lengths of cloth are:
- Cloth 1: 57 meters
- Cloth 2: 69 meters
- Cloth 3: 93 meters
1. Prime Factorization of 57:
- 57 can be divided by 3 (57 ÷ 3 = 19).
- Therefore, the prime factorization of 57 is:
57=3×19
- 69 can also be divided by 3 (69 ÷ 3 = 23).
- Therefore, the prime factorization of 69 is:
69=3×23
- 93 can again be divided by 3 (93 ÷ 3 = 31).
- Therefore, the prime factorization of 93 is:
93=3×31
From the prime factorizations:
- 57 = 3 × 19
- 69 = 3 × 23
- 93 = 3 × 31
Since 3 is the only common factor, the HCF of 57, 69, and 93 is:
HCF=3
The greatest measure (in meters) that can measure the lengths of cloth completely is:
Answer=3 meters
Topper's Solved these Questions
Similar Questions
Knowledge Check
The length of three rods is 64 cm., 80 cm. and 96 cm. Find the least length of a cloth which can be measured by using any of the three rods.
A0.96 m.B19.20 m.C9.60 m.D96 m.The reading of the ammeter and voltmeters are (Both the instruments are ac meters and measures rms value)-
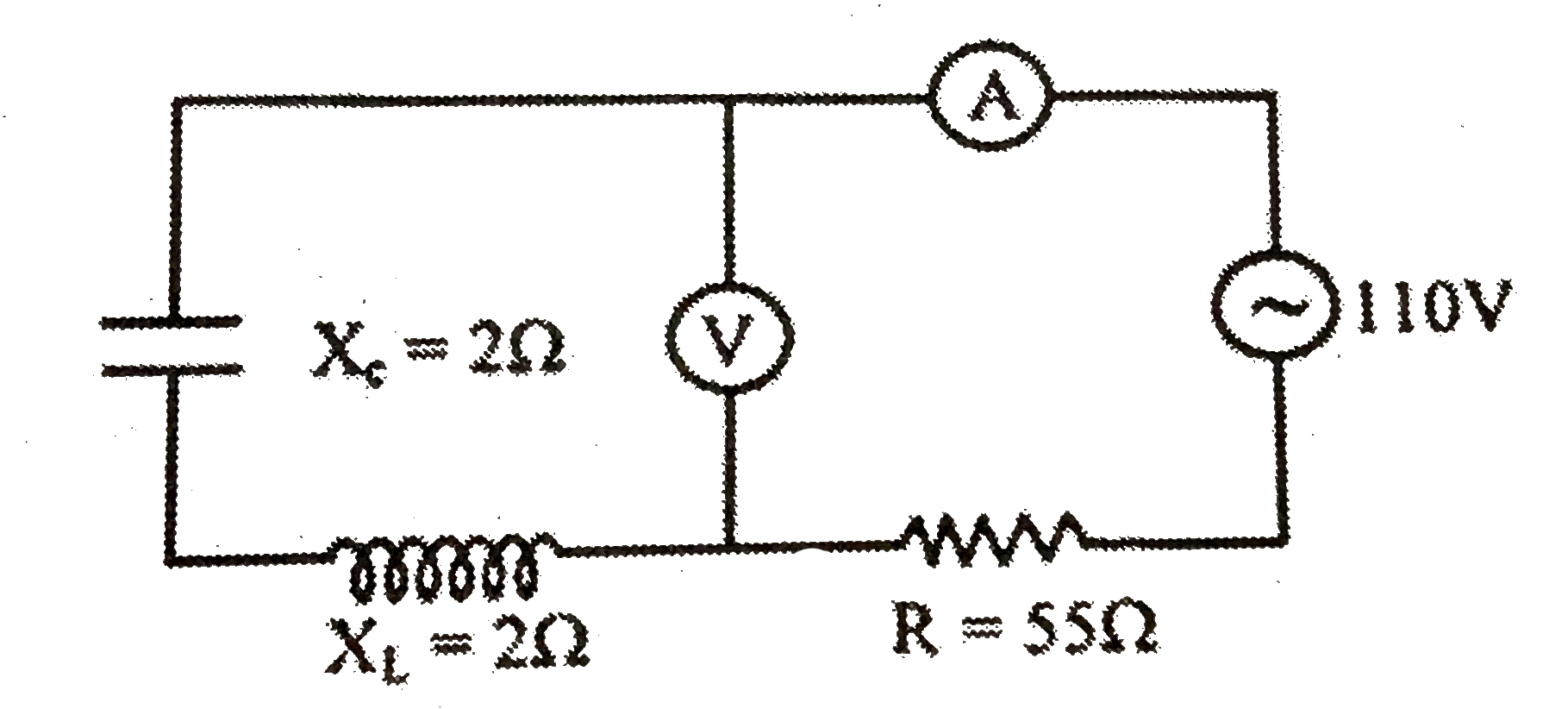 A2A,110VB2A,0VC2A,55VD1A,0V
A2A,110VB2A,0VC2A,55VD1A,0VGravity meter is used to measure
Aweight of bodyBgravitational constantCchanges in acceleration due to gravityDnone of these
What does the electricity meter measure?
View SolutionThe perimeter of a rectangle is 72 meters and its area is 315 square meters. Find the length of the rectangle
View SolutionThe meter that measures the speed of the vehicle is called _____.
View SolutionThe meter that measures the distance moved by the vehicle is called_____.
View SolutionThe diameter of the nucleus of an atom is measured in fermi (femto)meter (fm) which is equal to
View Solution
