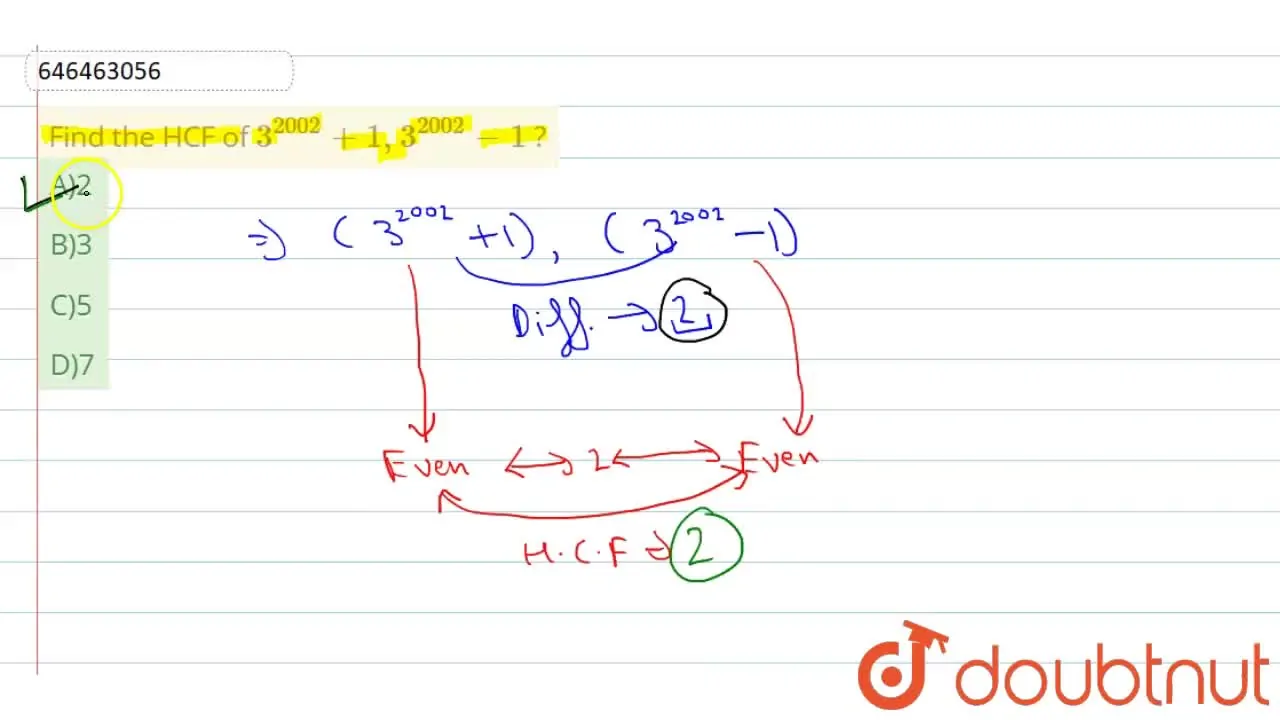
Find the HCF of 32002+1,32002−1 ?
A)2
B)3
C)5
D)7
The correct Answer is:A
Step by step video, text & image solution for Find the HCF of 3^(2002)+1,3^(2002)-1 ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Related Playlists
Similar Questions
Find the HCF of 3120−1,350−1 ?
View SolutionFind the HCF of 3100−1and3120−1.
View SolutionFind the HCF of 325+1,335+1 ?
View SolutionFind the HCF of (3125−1)and(335−1).
View Solution(a) Find the HCF of 28x4 and 70x6.
(b) Find the HCF of 48x2(x+3)2(2x−1)3(x+1) and 60x3(x+3)(2x−1)2(x+2).View Solution(a) Find the HCF of 28x4 and 70x6.
(b) Find the HCF of 48x2(x+3)2(2x−1)3(x+1) and 60x3(x+3)(2x−1)2(x+2).View SolutionFind the HCF of 12,34and45
View SolutionFind the HCF of a43.b52.c13 and a23.b34.c43
View SolutionNumber of cyphers at the end of ^(2002)C1001 is
View SolutionWhich of the following statement(s) is/are TRUE?
I. Highest common factor of (32002−1) and (32002+1) is 4 II.(484−1) is exactly divisivle by 5
निम्नलिखित में से कौन सा/से कथन सत्य है?
I. (32002−1) तथा (32002+1) का महत्त्म समापवर्तक 4 है । II.(484−1) 5 से पूर्णतः विभाजित है।View Solution