Three wooden blocks are of size 36 m, 54 m & 63 m respectively. They are to be divided into smaller blocks of equal size. What would be the size of smaller block ?
9 m.
18 m.
51 m.
4.5 m.
The correct Answer is:A
To find the size of the smaller block that can be obtained from the three wooden blocks of sizes 36 m, 54 m, and 63 m, we need to calculate the Highest Common Factor (HCF) of these three numbers. Here’s how to do it step by step:
Step 1: Prime Factorization
First, we will perform the prime factorization of each of the three numbers.
1. For 36:
- 36 can be divided by 2:
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
- So, the prime factorization of 36 is:
36=22×32
2. For 54:
- 54 can be divided by 2:
- 54 ÷ 2 = 27
- 27 ÷ 3 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
- So, the prime factorization of 54 is:
54=21×33
3. For 63:
- 63 can be divided by 3:
- 63 ÷ 3 = 21
- 21 ÷ 3 = 7
- 7 ÷ 7 = 1
- So, the prime factorization of 63 is:
63=32×71
Step 2: Identify Common Factors
Next, we identify the common prime factors and their lowest powers from the factorizations:
- The common prime factor among 36, 54, and 63 is 3.
- The powers of 3 in the factorizations are:
- For 36: 32
- For 54: 33
- For 63: 32
The lowest power of 3 common to all three numbers is 32.
Step 3: Calculate HCF
Now we can calculate the HCF by multiplying the common prime factors with their lowest powers:
HCF=32=9
Conclusion
Thus, the size of the smaller block that can be obtained from the three wooden blocks is 9 meters.
---
First, we will perform the prime factorization of each of the three numbers.
- 36 can be divided by 2:
- 36 ÷ 2 = 18
- 18 ÷ 2 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
- So, the prime factorization of 36 is:
36=22×32
- 54 can be divided by 2:
- 54 ÷ 2 = 27
- 27 ÷ 3 = 9
- 9 ÷ 3 = 3
- 3 ÷ 3 = 1
- So, the prime factorization of 54 is:
54=21×33
- 63 can be divided by 3:
- 63 ÷ 3 = 21
- 21 ÷ 3 = 7
- 7 ÷ 7 = 1
- So, the prime factorization of 63 is:
63=32×71
Next, we identify the common prime factors and their lowest powers from the factorizations:
- The powers of 3 in the factorizations are:
- For 36: 32
- For 54: 33
- For 63: 32
Now we can calculate the HCF by multiplying the common prime factors with their lowest powers:
Thus, the size of the smaller block that can be obtained from the three wooden blocks is 9 meters.
Topper's Solved these Questions
Similar Questions
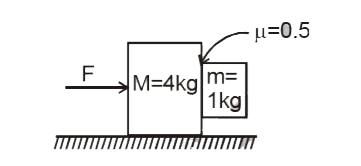
Find out the range of force for which smaller block is at rest with respect to bigger block.
View SolutionA block of mass m is kept over another block of mass M nd the system rests on a horizontal force F acting on the lower block produces an accelertion F2(m+M) in the system the two blocks always move together. A. Find the coefficient of kinetic frictioin between the bigger block and th horizontal surface. b. find the frictional force acting on the smaller block. c. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system.
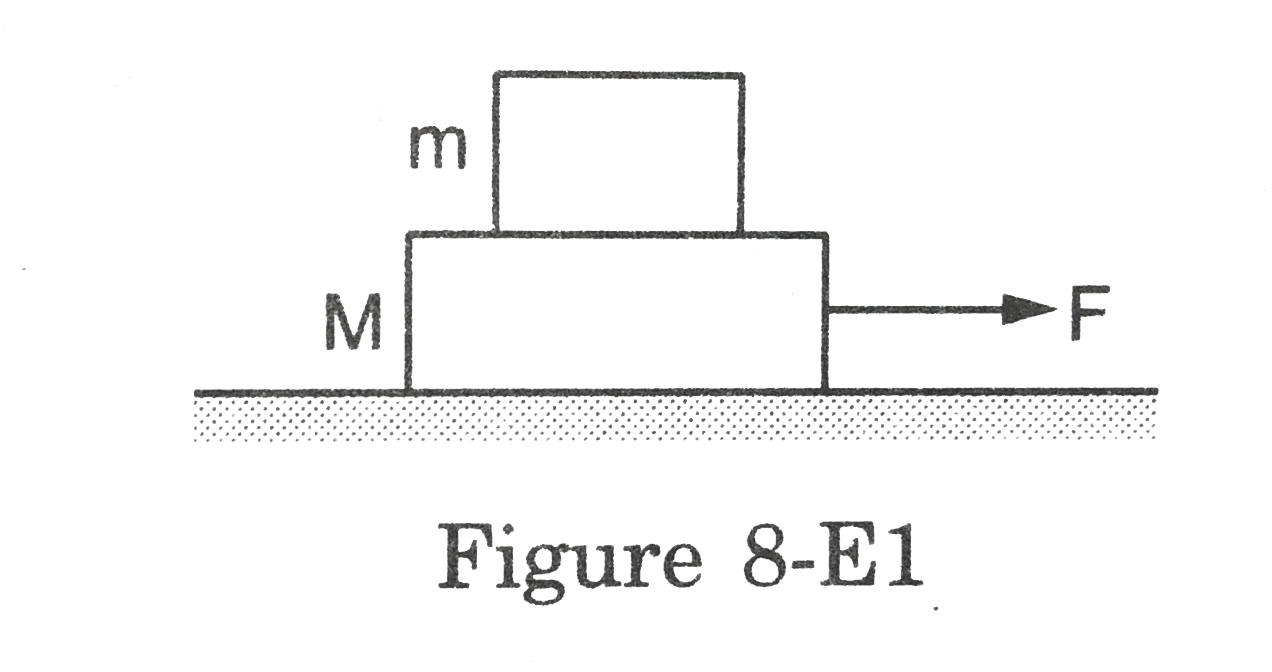
View Solution
Knowledge Check
If the magnification of a body of size 1 m is 2, what is the size of the image ?
A1.5 mB2.5 mC2 mD4 mThe dimensions of a wooden block are 1.1m×2.36m×3.1m. The number of significant figures in its volume should be
A1B2C3D4Assertion: Halides of Be dissolve in organic solvents
Reason: Atomic size of Be is smaller in the s-block elements.AIf both Assertion & Reason are True & the Reason is a correct explanation of the AssertionBIf both Assertion & Reason are True but Reason is not a correct explanation of the AssertionCIf Assertion is True but the Reason is FalseDIf both Assertion & Reason are False
A block of mass m is kept over another block of mass M and the system rests on a horizontal surface. A constant horizontal force F acting on the lower block produces an acceleration F2(m+M) in the sytem. The two blocks always move together. Consider displacement d of the system.
a. Find the work done by friction on bigger block.
b. Find the coefficient of kinetic friction between the bigger block and the horizontal surface.
c. Find the frictional acting on the smaller block.
d. Find the work done by the force of friction on the smaller block by the bigger block.
e. Find the work done by static friction on bigger block.
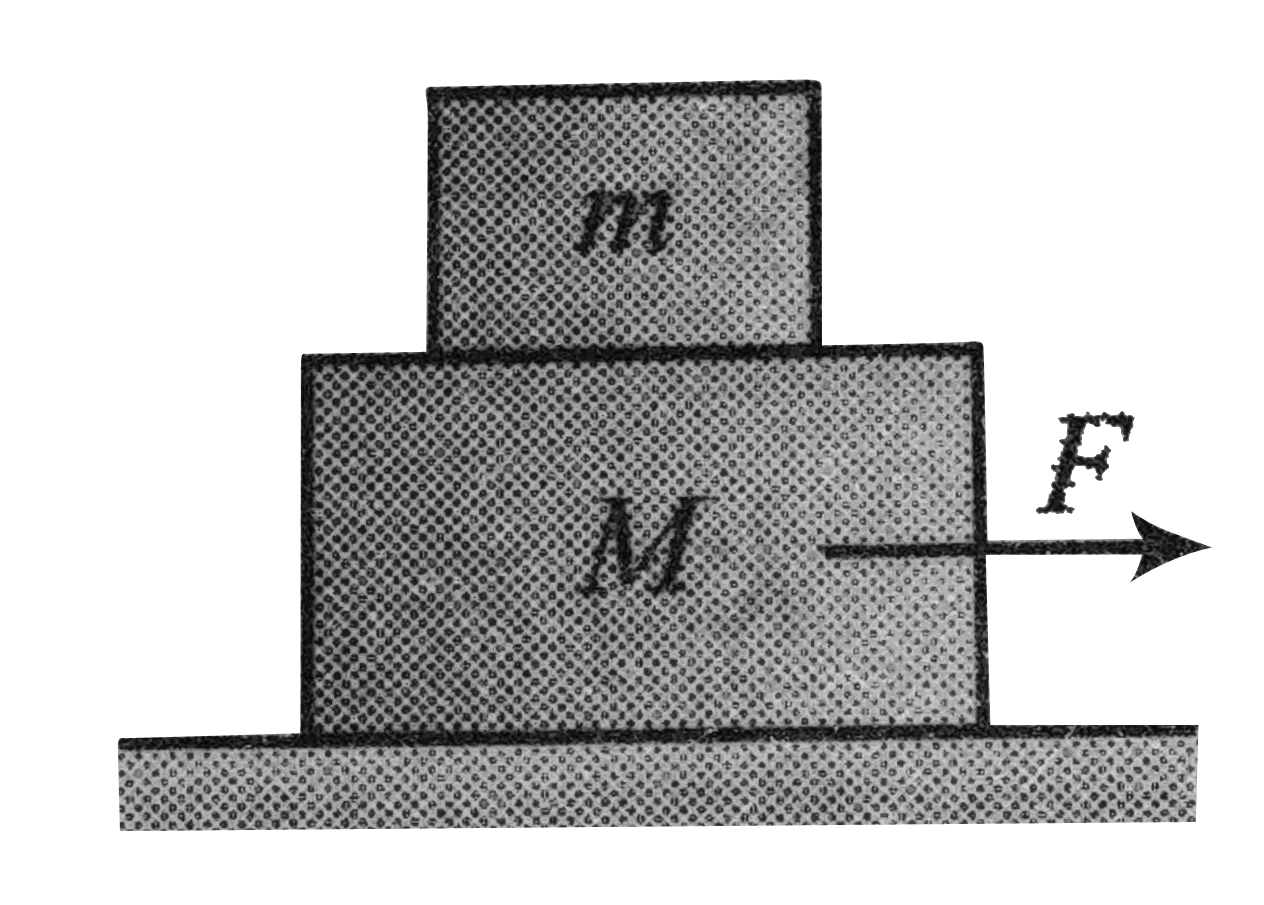
View SolutionIf size of an atom (≈10−10m) is scaled up to 1m, what would be the size of nucleus (≈10−14m)?
View SolutionThe weight of a metal block of size 5 cm by 4 cm by 3 cm is 1 kg. Find the weight of a block of the same metal of size 15 cm by 8 cm by 3 cm.
View SolutionWhen we ignore friction and mass of pulley what would be the accelerations of the two blocks m1 and m2
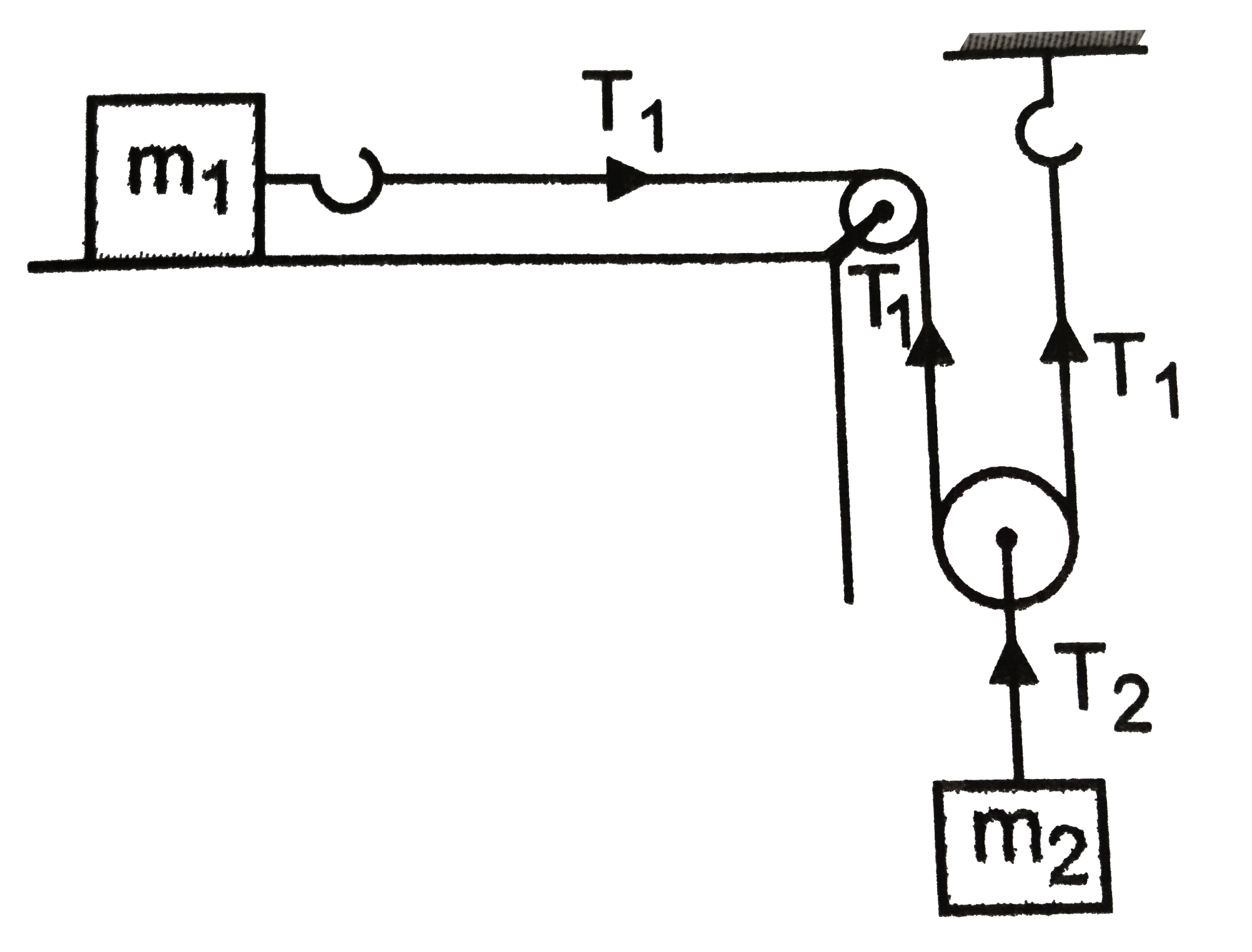 .
.
View SolutionTwo blocks A and B of mass mAandmB respectively are kept in contact on a frictionless table. The experimenter pushes the block A from behind so that the blocks accelerate. If the block A exerts a fore F on the block B, what is the force exerted by the experimenter on A?
View Solution
