A ray of light incident on a transparent sphere at an angle π/4 and refracted at an angle r, emerges from the sphere after suffering one internal reflection. The total angle of deviation of the ray is
3π2−4r
π2−4r
π4−r
5π2−4r
The correct Answer is:A
To solve the problem, we will analyze the path of the ray of light as it enters and exits the transparent sphere, taking into account the angles of incidence, refraction, and reflection.
Step 1: Identify the angles
The ray of light is incident on the sphere at an angle of π4. Let the angle of refraction inside the sphere be r.
Step 2: Apply Snell's Law at the first interface
Using Snell's law at the point of incidence:
n1sin(θ1)=n2sin(r)
Assuming the sphere is in air, n1=1 (air) and n2 is the refractive index of the sphere. Thus:
sin(π4)=n2sin(r)
This gives us:
1√2=n2sin(r)(1)
Step 3: Internal Reflection
After refraction, the ray travels inside the sphere and strikes the opposite side. The angle of incidence at this point is r. According to the law of reflection, the angle of reflection will also be r.
Step 4: Calculate the angle of emergence
The ray will then refract out of the sphere at the same angle r (due to symmetry). Thus, the angle of emergence will also be π4.
Step 5: Calculate the total angle of deviation
The total angle of deviation D can be calculated by considering the angles involved:
1. The ray wanted to go straight but deviated at the first interface, which gives a deviation of:
D1=π4−r
2. After internal reflection, the ray again deviates when it exits the sphere:
D2=π−2r
3. Finally, the ray deviates again when it exits:
D3=π4−r
Step 6: Combine the deviations
The total deviation D is the sum of all deviations:
D=D1+D2+D3=(π4−r)+(π−2r)+(π4−r)
Combining these:
D=π4+π4+π−4r=3π2−4r
Final Answer
The total angle of deviation of the ray is:
D=3π2−4r
The ray of light is incident on the sphere at an angle of π4. Let the angle of refraction inside the sphere be r.
Using Snell's law at the point of incidence:
n1sin(θ1)=n2sin(r)
Assuming the sphere is in air, n1=1 (air) and n2 is the refractive index of the sphere. Thus:
sin(π4)=n2sin(r)
This gives us:
1√2=n2sin(r)(1)
After refraction, the ray travels inside the sphere and strikes the opposite side. The angle of incidence at this point is r. According to the law of reflection, the angle of reflection will also be r.
The ray will then refract out of the sphere at the same angle r (due to symmetry). Thus, the angle of emergence will also be π4.
The total angle of deviation D can be calculated by considering the angles involved:
1. The ray wanted to go straight but deviated at the first interface, which gives a deviation of:
D1=π4−r
2. After internal reflection, the ray again deviates when it exits the sphere:
D2=π−2r
3. Finally, the ray deviates again when it exits:
D3=π4−r
The total deviation D is the sum of all deviations:
D=D1+D2+D3=(π4−r)+(π−2r)+(π4−r)
Combining these:
D=π4+π4+π−4r=3π2−4r
The total angle of deviation of the ray is:
D=3π2−4r
Topper's Solved these Questions
- QUESTION PAPER 2013Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2013Exercise:PART-I ( PHYSICS)
Explore 20 Videos
- QUESTION PAPER 2013Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2013Exercise:PART-II ( PHYSICS)
Explore 10 Videos
- QUESTION PAPER 2013Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2013Exercise:PART-II ( PHYSICS)
Explore 10 Videos
- MOCK TEST 9Book:KVPY PREVIOUS YEARChapter:MOCK TEST 9Exercise:EXERCISE
Explore 19 Videos
- QUESTION PAPER 2020Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2020Exercise:PART-I : PHYSICS
Explore 50 Videos
Similar Questions
The path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
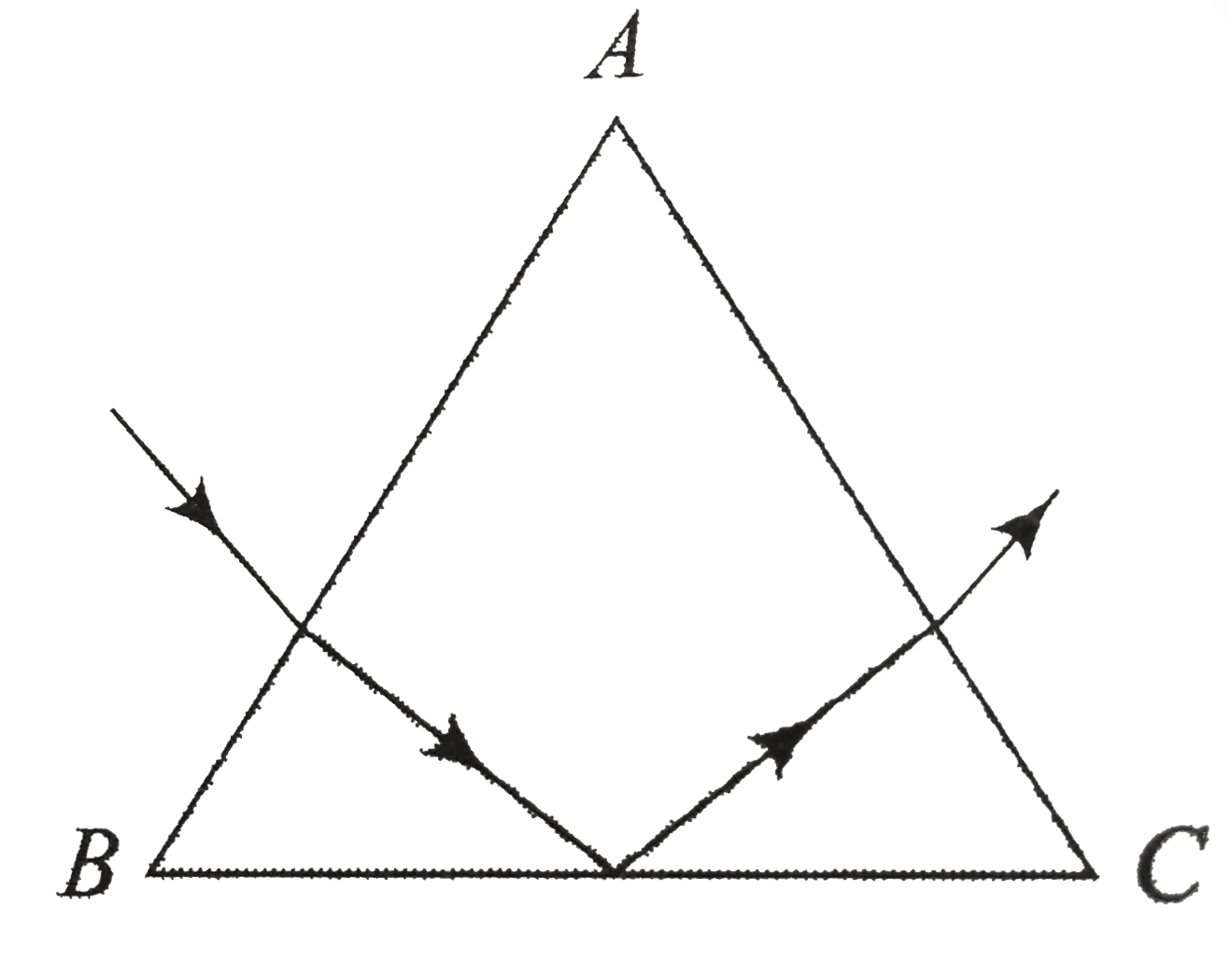
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View Solution
Knowledge Check
A monochromatic ray of light is incident normally on one of the refracting surfaces of a prism . The emergent ray grazes the second refracting surface . What is the angle of the prism if the refractive index of the material of the prism is 1.6 ?
AA<2CBA = 2CCA>2CDA<C2A ray of light incident on a transparent block at an angle of incident 60∘. If the refractive index of the block is 1.732, the angle of deviation of the refracted ray is
A15∘B25∘C30∘D45∘A ray of light is incident on a plane mirror at an angle of incidence 40∘. The ray, after reflection, is deviated through
A30∘B60∘C90∘D100∘
A ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60° so that it just suffers total internal reflection at the other face ? The refractive index of the material of the prism is 1.524.
View SolutionA light ray is incident on a glass sphere at an angle of incidence 60∘ as shown. Find the angles r, r', e and the total deviation after two refractions.

View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60∘, so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
View SolutionAt what angle should a ray of light be incident on the face of a prism of refracting angle 60∘ so that it just suffers total internal reflection at the other face ? The refractive index of the prism is 1.524.
View Solution