Figure below shows a shampoo bottle in a perfect cylindrical shape
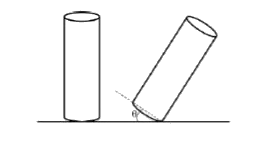
In a simple experiment, the stability of the bottle filled with different amount of shampoo volume is observed. The bottle is tilted from one side and then released. Let the angle depicts the critical angular displacement resulting in the bottle losing its stability and tripping over. Choose the graph correctly depicting the fraction f of shampoo filled (f= 1 corresponds to completely filled) vs the tripping angle
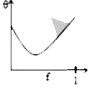
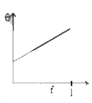
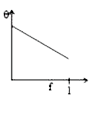
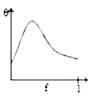
The correct Answer is:D
Mass of bottle =
Length of bottle = L
base Area = A =
density of shampoo = p
mass of shampoo = pfAL

Center of mass of system
for critical angular displacement, mg will pass through tilted side.

From the diagram
at f = 0 & f = 1, tipping angle ‘’ will be same. for very small values of ‘f’, we can neglect terms
So if f increases will increase.
Topper's Solved these Questions
Similar Questions
Knowledge Check
cork/bottle cork is formed from
Acork cambium ( phellogon)Bvascular cambiumCphloemDxylemA bottle of glue lying on its base is in:
Astable equilibriumBunstable equilibriumCneutral equilibriumDdynamic equilibriumA bottle is full of dettol. One-third of it is taken out and then an equal amount of water is poured into the bottle to fill it. This operation is done four times. Find the final ratio of dettol and water in the bottle
A13:55B20:74C16:65D10:48
Take an empty bottle of the sort in which bottled water is sold. Pour about 5-10 mL of water into it and close the bottle tightly. Shake it well or leave it out in the Sun for ten minutes. This causes the air in the bottle to be saturated with water vapour. • Now, take a lighted incense stick. Open the cap of the bottle and allow some of the smoke from the incense stick to enter the bottle. Quickly close the bottle once more. Make sure that the cap is fitting tightly. Press the bottle hard between your hands and crush it as much as possible. Wait for a few seconds and release the bottle. Again press the bottle as hard as you can.
What is the need for smoke particles inside the bottle for this experiment?
View SolutionWhen hot water is placed into an empty water bottle, the bottle keeps its shape and does not soften. What type of plastic is the water bottle made from?
View SolutionA bottle is full of dettol .One third if it , is taken out and then equal amount of water is poured into the bottle to fill it .This operation is done four times .Find the final ratio of dettol and water in the bottle .
View SolutionAn empty plastic bottle is kept and three holes are made in it at the same height from the bottom of the bottle. Bottle is now filled with water. Water stands leaking out 'from the holes. Do the different stream of water coming out of the holes fall at the same distance from the bottle? What conclusion do you draw ?

View SolutionThe mass of a bottle filled with water is found to be 150 g. the mass of the empty bottle is 50 g and the external volume of the container is 125 cm3. Find out the density of the material of the bottle.
View Solution
