Consider a regular 10-gon with its vertices on the unit circle. With one vertex fixed, draw straight lines to the other 9 vertices. Call them L1,L2,…,L9 and denote their lengths by l1,l2,…,l9 respectively. Then the product l1,l2,...,l9 is
10
10√3
50√3
20
The correct Answer is:A
To solve the problem, we need to find the product of the lengths of the lines drawn from a fixed vertex of a regular 10-gon inscribed in a unit circle to the other 9 vertices. Let's denote the vertices of the 10-gon as V0,V1,V2,…,V9 where V0 is the fixed vertex.
1. Identify the vertices: The vertices of the regular 10-gon can be represented in the complex plane as:
Vk=ei2πk10for k=0,1,2,…,9
Here, V0 is fixed, and we will calculate the lengths to the other vertices V1,V2,…,V9.
2. Calculate the lengths: The length lk from the fixed vertex V0 to vertex Vk is given by:
lk=|V0−Vk|=|1−ei2πk10|for k=1,2,…,9
3. Express the lengths: The lengths can be rewritten as:
lk=|1−ei2πk10|=√(1−cos(2πk10))2+sin2(2πk10)
Using the identity sin2x+cos2x=1, we simplify this to:
lk=√2−2cos(2πk10=2sin(πk10)
4. Product of lengths: We need to find the product:
P=l1⋅l2⋅…⋅l9=(2sin(π10))⋅(2sin(2π10))⋅…⋅(2sin(9π10))
This can be factored as:
P=29⋅sin(π10)⋅sin(2π10)⋯sin(9π10)
5. Using the product-to-sum identity: The product of sines can be evaluated using the identity:
sinxsin(π−x)=sin2x
This means:
sin(9π10)=sin(π10),sin(8π10)=sin(2π10),…
Thus, the product simplifies to:
P=29⋅(sin(π10))5⋅(sin(2π10))4
6. Final result: The product of the lengths l1,l2,…,l9 is:
P=10
Conclusion:
The product l1⋅l2⋯l9 is equal to 10.
Vk=ei2πk10for k=0,1,2,…,9
Here, V0 is fixed, and we will calculate the lengths to the other vertices V1,V2,…,V9.
lk=|V0−Vk|=|1−ei2πk10|for k=1,2,…,9
lk=|1−ei2πk10|=√(1−cos(2πk10))2+sin2(2πk10)
Using the identity sin2x+cos2x=1, we simplify this to:
lk=√2−2cos(2πk10=2sin(πk10)
P=l1⋅l2⋅…⋅l9=(2sin(π10))⋅(2sin(2π10))⋅…⋅(2sin(9π10))
This can be factored as:
P=29⋅sin(π10)⋅sin(2π10)⋯sin(9π10)
sinxsin(π−x)=sin2x
This means:
sin(9π10)=sin(π10),sin(8π10)=sin(2π10),…
Thus, the product simplifies to:
P=29⋅(sin(π10))5⋅(sin(2π10))4
P=10
The product l1⋅l2⋯l9 is equal to 10.
Topper's Solved these Questions
- QUESTION PAPER 2020Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2020Exercise:PART-II(MATHEMATICS)
Explore 10 Videos
- QUESTION PAPER 2020Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2020Exercise:PART-II : MATHEMATICS
Explore 7 Videos
- QUESTION PAPER 2013Book:KVPY PREVIOUS YEARChapter:QUESTION PAPER 2013Exercise:PART-II ( MATHEMATICS)
Explore 10 Videos
- SOLVED PAPER 2018Book:KVPY PREVIOUS YEARChapter:SOLVED PAPER 2018Exercise:EXAMPLE
Explore 27 Videos
Similar Questions
Knowledge Check
In Fig., there are two convex lenses L1andL2 having focal lengths F1 and F2 respectively. The distance between L1 and L2 will be :
 .AF1BF2CF1+f2DF1−F2
.AF1BF2CF1+f2DF1−F2The area of the triangle whose vertices are A (1,2,3) B (2,−l,l) and C (l,2,−4) is
A7√10squnitsB12√10squnitsC72√10squnitsDNone of the theseIn the figure given below there are two convex lenses L1 and L2 having focal lengths F1 and F2 respectively. The distance between L1 and L2 will be
 AF1BF2CF1+F2DF1−F2
AF1BF2CF1+F2DF1−F2
Questions based on L1 and L2
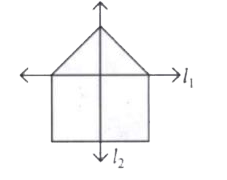
View SolutionFor the given figure, which one is the mirror line, l1 or l2?
View SolutionLet R be the relation over the set of all straight lines in a plane such that l1Rl2⇔l1⊥l2. Then, R is
View SolutionLet L be the set of all straight lines in the Euclidean plane. Two lines l1 and l2 are said to be related by the relation R iff l1 is parallel to l2. Then, the relation R is not
View SolutionLet L be the set of all straight lines in the Euclidean plane. Two line l1 and l2 are said to be related by the relationR of l1 is parallel to l2, Then R is
View Solution