Given A=⎡⎢⎣111241231⎤⎥⎦,B=[2334]. Find P such that BPA= [101010] Solution in Punjabi
Given, BPA=[101010]
∴ p=b−1[101010]A−1
∴ B=[2334]⇒B−1=1(−1)[4−3−32]=[−433−2]
∴ B−1=[−433−2]
and A=[(1,1,1),(2,4,1),(2,3,1)
∴ |A|=1(4−3)−1(2−2)+1(6−8)=−1≠0
Now, adj A=⎡⎢⎣12−30−11−2−12⎤⎥⎦
∴ A−1=adjA|A|=⎡⎢⎣−1−2301−121−2⎤⎥⎦
substiruting the values of A−1 and B−1 from Eqs. (ii) and (iii) in Eq. (i), then
P=[−433−2][101010]⎡⎢⎣−1−2301−121−2⎤⎥⎦
P=[−433−2][1−1101−1][−47−73−55]
Topper's Solved these Questions
- MATRICES Book:ARIHANT MATHSChapter:MATRICES Exercise:Exercise For Session 1
Explore 9 Videos
- MATRICES Book:ARIHANT MATHSChapter:MATRICES Exercise:Exercise For Session 2
Explore 19 Videos
- MATHEMATICAL INDUCTION Book:ARIHANT MATHSChapter:MATHEMATICAL INDUCTION Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 2 Videos
- MONOTONICITY MAXIMA AND MINIMABook:ARIHANT MATHSChapter:MONOTONICITY MAXIMA AND MINIMAExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 31 Videos
Similar Questions
If A=∣∣∣α22α∣∣∣and|A|3=125 , then the value of α is a.±1 b. ±2 c. ±3 d. ±5
View SolutionIf A=[4x+22x−3x+1] is symmetric, then x =
View SolutionIf t₁+t₅+t15+t₁₀+t₂₀+t₂₄=225 Find the sum of first 24th term of that A.P?
View SolutionThe least value of α∈R for which 4ax2+1x≥1, for all x>0, is
View SolutionThe truth table given below is for: |(A,B,X),(0,0,0),(0,1,0),(1,0,0),(1,1,1)|
View SolutionThe truth table shown below in and belong to which gates? (a) |{:(A,B,Y),(0,0,0),(0,1,0),(1,0,0),(1,1,1):}| (b) |{:(A,B,Y),(0,0,1),(1,0,1),(0,1,1),(1,1,0):}|
View SolutionIf A=⎡⎢⎣100101010⎤⎥⎦, then
View Solutionएक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष बिंदु A(1,1,1),B(1,2,3) और C(2,3,1) है!
View Solutionयदि A=⎡⎢⎣231132123⎤⎥⎦ तथा B=⎡⎢⎣412241142⎤⎥⎦ हो, तो सिद्ध कीजिये कि (A+B)'=A'+B'
View SolutionEquation of the plane passing through the points (1,0,1), (-1,1,1) and (2,3,1) is
View SolutionThe truth table for the following combination of gates is
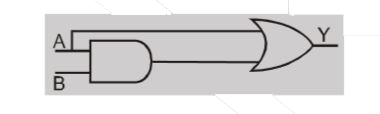
(a) ABY000010101111
(b) ABY000010100111
(c) ABY001011101110
(d) ABY0000111011110
View SolutionIf A=⎡⎢⎣100101010⎤⎥⎦ Then tra(A)
View SolutionIf A=⎡⎢⎣111241231⎤⎥⎦,B=[2334] then the matrix BA is
View Solutionएक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष बिन्दु A(1,1,1),B(1,2,3) और C(2,3,1) है।
View SolutionIf A = ⎡⎢⎣110010101⎤⎥⎦ then A3 =
View SolutionIf A = ⎡⎢⎣110010101⎤⎥⎦ then A3 =
View Solution