The value of b for which the equation 2log1/25(bx+28)=−log5(12−4x−x2) has coincident roots isSolution in Punjabi
The correct Answer is:4
Step by step video, text & image solution for The value of b for which the equation 2 log_(1//25)(bx+28)=- log_(5) (12-4x-x^(2)) has coincident roots is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Matching Type Questions)
2 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise for session 8
1 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Passage Based Questions)
12 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise For Session 6
5 Videos
- MATHEMATICAL INDUCTION BOOK - ARIHANT MATHSCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
Similar Questions
Every Integer is Natural number ?
View Solution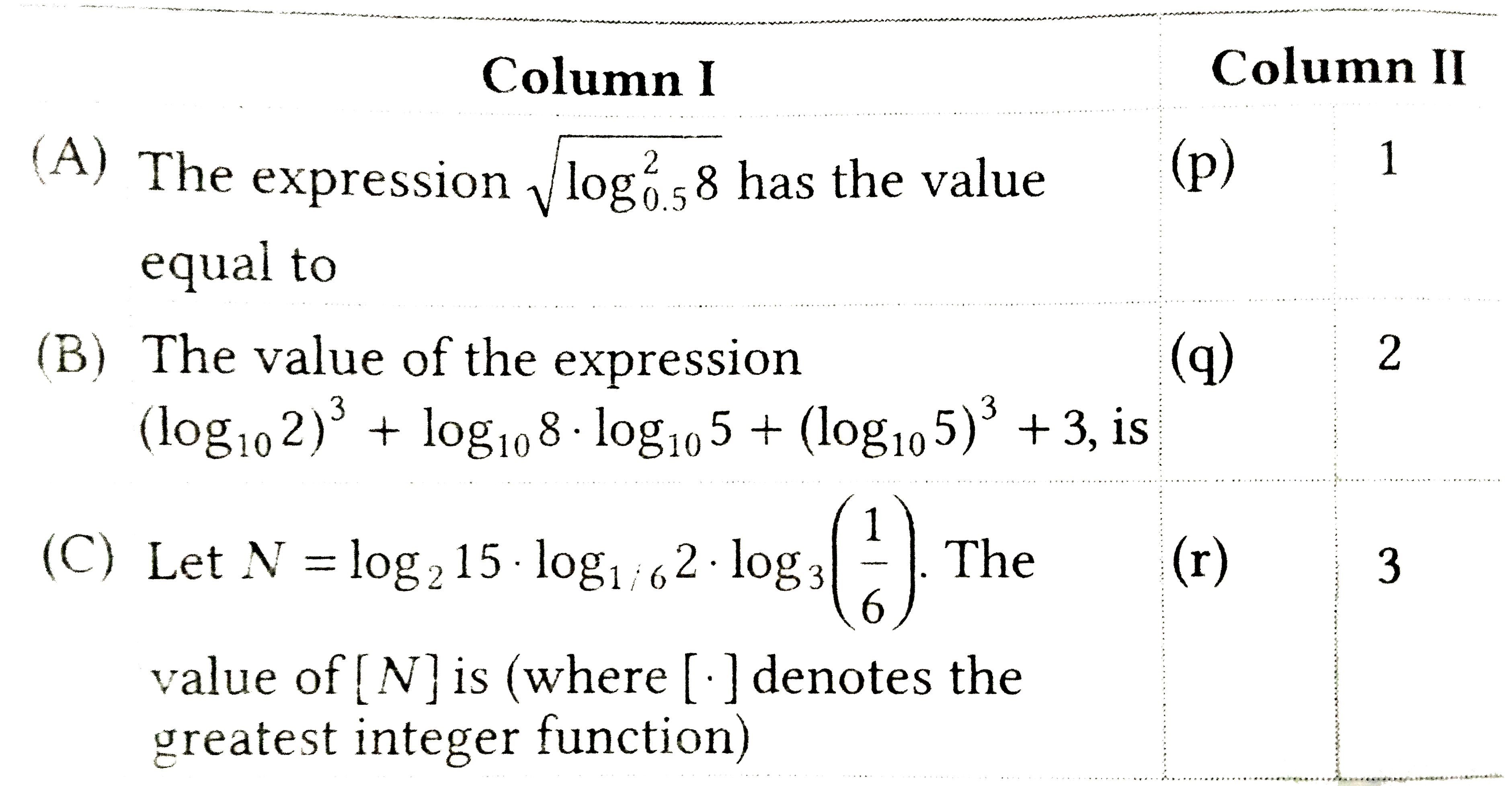

View SolutionFind dydxify=cos(logx)
View SolutionThe value o limx→∞(1n3)([12x+12]+[22x+22]+…..+[n2x+n2]) is where [.] denotes the greatest integer function.
View SolutionIf t₁+t₅+t15+t₁₀+t₂₀+t₂₄=225 Find the sum of first 24th term of that A.P?
View SolutionThe value of x for which the equation 5⋅3log3x−21−log2x−3=0
View SolutionIf a and b are the solutions of equation log_(5)(log_(64)(|x|)-(1)/(2)+25^(x))=2x then
View SolutionSolve the equation,log_(x^(2)+4x+5){log_(3x^(2)+4x+5)(x^(2)-3x)}=0
View SolutionIf a=log_(12)5 and b=log_(25)3, then log_(5)2 is equal to
View SolutionThe number of value of x satisfying 1+log_(5)(x^(2)+1)>=log_(5)(x^(2)+4x+1) is
View SolutionThe roots of the equation log_(2)(x^(2)-4x+5)=(x-2) are
View SolutionIf log5(x2+x)−log5(x+1)=2, then the value of x is a. 5 b. 10 c. 25 d. 32
View SolutionIf the product of the roots of the equation,x((3)/(4))(log_(2)x)^(2)+log_(2)x-(5)/(4)=sqrt(2) is (1)/((a)^((1)/(b))) (where a,b in N ) then the value of (a+b)
View SolutionSum of squares of the roots of the equation slogs 5^(log_(5)(x^(2)-4x+5))=x-1 is equal to
View SolutionIf x1 and x2 are solution of the equation log5(log64|x|+(25)x−12)=2x, then
View SolutionThe sum of all the roots of the equation log2(x−1)+log2(x+2)−log2(3x−1)=log24
View Solution
