Leta1,a2,.... be in AP and q1,q2,.... be in GP. If a1=q1=2 and a10=q10=3, then Solution in Punjabi
a7q19 is not an integer
a19q7is an integer
a7q19=a19q10
None of these
The correct Answer is:C
a1,a2,...., are in AP and q1,q2,...., are in GP.
a1=q1=2 and a10=q10=3
Let d be the common difference of AP
i.e.,d=3−29=19
Then, a7=a1+6d=2+6d=2+6×19=83
a19=a1+18d=2+18d
=2+18×19=369=4
Let r be the common ratio of GP i.e.,r=(32)19
Then, q7=q1r6=2r6b
=2⋅(32)6×19=2(32)23
q10=q1r9=2r9=2⋅(32)9×19=3
q19=q1⋅r18=2r18
=2⋅(32)18×19=2(32)189=92
a7=q19=83×92=12,a19=q10=4×3=12
Topper's Solved these Questions
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Passage Based Questions)
24 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise For Session 7
7 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHSCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
For a positive integer n let a(n)=1+12+13+14+.....+1(2n)−1. Then
View SolutionFind the value of x of equation 4x2=16
View SolutionThe minimum value of 4x+42−x,x∈R is
View SolutionProve that 2sin2(π6)−sec2(π3)=−72
View SolutionLet R={(3,3),(6,6),(9,9),(6,12),(3,9),(3,12),(12,12),(3,6)} is a relation on set A={3,6,9,12} then R is a) an equivalence relation b) reflexive and symmetric only c) reflexive and transitive only d) reflexive only
View Solutionlet a_(1),a_(2),a_(3)...... be an AP such that (a_(1)+a_(2)+............+a_(p))/(a_(1)+a_(2)+............+a_(q))=(p^(3))/(q^(3)) then a_(/)a_(21)
View SolutionTwo concentric sphere of radii a1 and a2 carry chages q1 and q2 respectively.If the surface charge density (σ) is same for both spheres,the electric potential at the common centre will be
View SolutionCalculate Q1,Q2andQ3,

View Solutionदो गोलीय चालक A1 तथा A2 की त्रिज्याएँ क्रमश: r1 तथा r2 है । चालक A1 व A2 पर क्रमश: q1 तथा q2 आवेश हैं। चित्र के अनुसार चालकों को हवा में एक ताँबे की द्वारा जोड़ा जाता है । इस निकाय की तुल्य धारिता होगी -
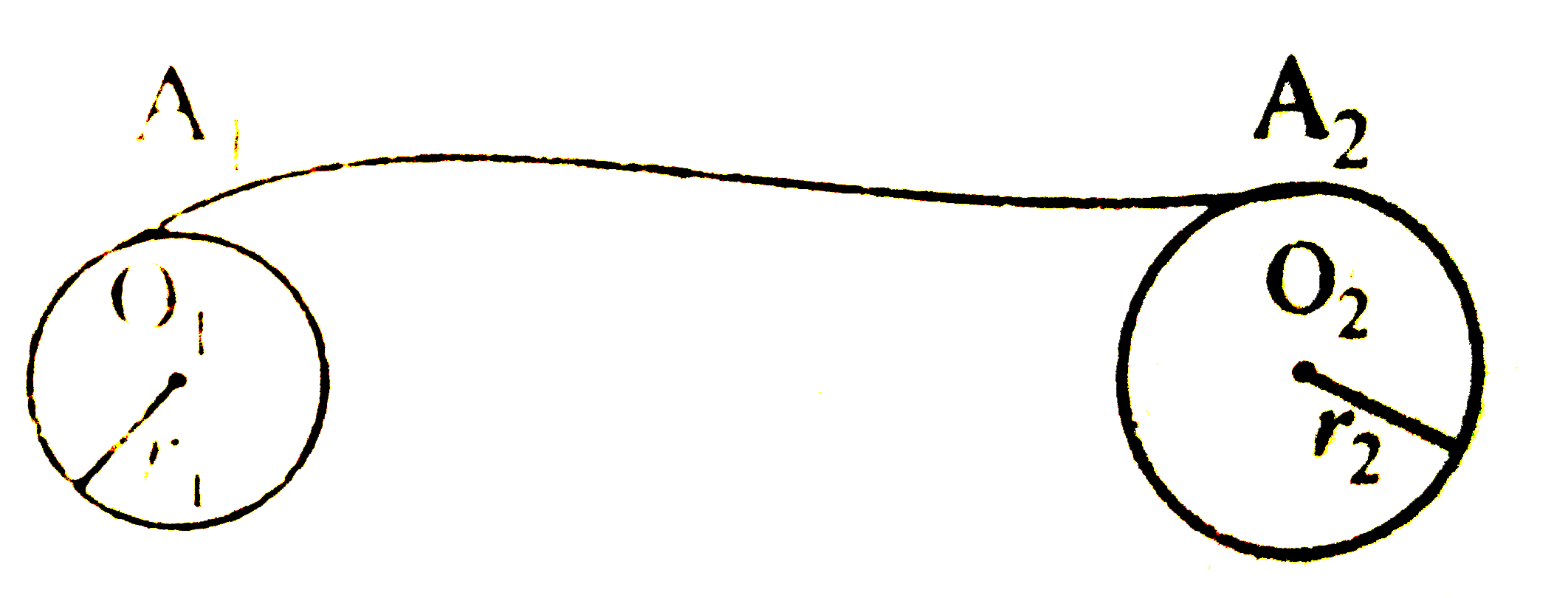
View SolutionIf a1,a2,a3,…. are in A.P., then ap,aq,qr are in A.P. if p,q,r are in
View Solutionif x,y and z are not all zero and connected by the equations a1x+b1y+c1z=0,azx+b2y+c2z=0 and (p1+λq1)x+(p2+λq2)y+(p3+λq3)z=0 show that
λ=−∣∣ ∣ ∣∣a1b1c1a2b2c2p1p2p3∣∣ ∣ ∣∣÷∣∣ ∣ ∣∣a1b1c1a2b2c2q1q2q3∣∣ ∣ ∣∣
View SolutionIf q1,2,q3 are roots of the equation x3+64=0, then the value of ∣∣ ∣ ∣∣q1q2q3q2q3q1q3q1q2∣∣ ∣ ∣∣ is :-
View SolutionA1,A2,…,An are independent events such that P(Ai)=1−qi,i=1,2,…,n. Prove that,
P(A1∪A2∪…∪An)=1−q1q2…qn.
View SolutionIf Q1,Q2,Q3,Q4 are the quadrants in a Cartesian plane then Q2∩Q3 is ________.
View SolutionIf a1,a2,...,.,a10 are positive numbers in arithmetic progression such that 1a1a2+1a2a3+...⋅+1a9a10=964 and 1a1a10+1a2a9+......1a10a1=110(1a1+...+1a10) then the value of 25(a1a10+a10a1) is
View SolutionSuppose a ∈ R and a≠0 . Let
P=⎡⎢⎣100a10a2a1⎤⎥⎦ and Q=(aij)
be 3×3 matrices such that Q−P5=I3. If q21+q31q32=12.1 then a = _____
View Solution
