If q1,q2,q3 ar rootsof the equation x3+64=0 then value of ∣∣ ∣ ∣∣q1q2q3q2q3q1q3q1q2∣∣ ∣ ∣∣
1
4
16
0
The correct Answer is:D
To solve the problem, we need to evaluate the determinant of the following matrix formed by the roots q1,q2,q3 of the equation x3+64=0:
D=∣∣
∣∣q1q2q3q2q3q1q3q1q2∣∣
∣∣
Step 1: Find the roots of the equation
The given equation is:
x3+64=0
This can be rewritten as:
x3=−64
Taking the cube root, we find:
x=−4
The roots of the equation are the cube roots of −64. The three roots are:
q1=−4,q2=4(cos2π3+isin2π3),q3=4(cos4π3+isin4π3)
Calculating these, we have:
q2=4(−12+i√32)=−2+2i√3
q3=4(−12−i√32)=−2−2i√3
Step 2: Calculate the determinant
Now we need to calculate the determinant D:
D=∣∣
∣∣q1q2q3q2q3q1q3q1q2∣∣
∣∣
Step 3: Simplify the determinant
We can simplify the determinant by adding all rows together. Let's denote the sum of the roots:
S=q1+q2+q3
Since q1,q2,q3 are the roots of the polynomial x3+64=0, we can find S:
Using Vieta's formulas, the sum of the roots S is given by:
S=−coefficient of x2coefficient of x3=−01=0
Step 4: Substitute back into the determinant
Now, we substitute S back into the determinant:
D=∣∣
∣∣Sq2q3q2q3Sq3Sq2∣∣
∣∣=∣∣
∣∣0q2q3q2q30q30q2∣∣
∣∣
Since the first row contains a zero, the determinant simplifies to zero:
D=0
Final Answer
Thus, the value of the determinant is:
0
∣∣q1q2q3q2q3q1q3q1q2∣∣
∣∣
The given equation is:
q3=4(−12−i√32)=−2−2i√3
Now we need to calculate the determinant D:
∣∣q1q2q3q2q3q1q3q1q2∣∣
∣∣
We can simplify the determinant by adding all rows together. Let's denote the sum of the roots:
Now, we substitute S back into the determinant:
∣∣Sq2q3q2q3Sq3Sq2∣∣
∣∣=∣∣
∣∣0q2q3q2q30q30q2∣∣
∣∣
Thus, the value of the determinant is:
Topper's Solved these Questions
Similar Questions
If q1,2,q3 are roots of the equation x3+64=0, then the value of ∣∣ ∣ ∣∣q1q2q3q2q3q1q3q1q2∣∣ ∣ ∣∣ is :-
View SolutionA=⎡⎢⎣l1m1n1l2m2n2l3m3n3⎤⎥⎦ and B=⎡⎢⎣p1q1r1p2q2r2p3q3r3⎤⎥⎦
Where pi,qi,ri are the co-factors of the elements li,mi,ni for i=1,2,3. If (l1,m1,n1),(l2,m2,n2) and (l3,m3,n3) are the direction cosines of three mutually perpendicular lines then (p1,q1,r1),(p2,q2,r2) and (p3,q,r3) are
View Solution
Knowledge Check
If Q1=20,Q3=48, then coefficient of quartile deviation is :
A28B68C717D617If semi Inter quartile range is 19.38,Q3=72.5 then , Q1 is
A(a)38.75B(b)35.75C(c)33.74D(d)34.75
If each pair of the three equations x2−p1x+q1=0,x2−p2c+q2=0,x2−p3x+q3=0 have common root, prove that, p21+p22+p23+4(q1+q2+q3)=2(p2p3+p3p1+p1p2)
View SolutionThe roots of the equation (q−r)x2+(r−p)x+p−q=0 are (A) r−pq−r,1 (B) p−qq−r,1 (C) q−rp−q,1 (D) r−pp−q,1
View SolutionThe value of p and q(p≠0,q≠0) for whichp,q are the roots of the equation x2+px+q=0 are (a)p=1,q=−2 (b) p=−1,q=−2 (c) p=−1,q=2 (d) p=1,q=2
View SolutionThe vertices of a triangle are (pq,1pq),(pq)),(qr,1qr), and (rq,1rp), where p,q and r are the roots of the equation y3−3y2+6y+1=0 . The coordinates of its centroid are (1,2) (b) (2,−1) (c) (1,−1) (d) (2,3)
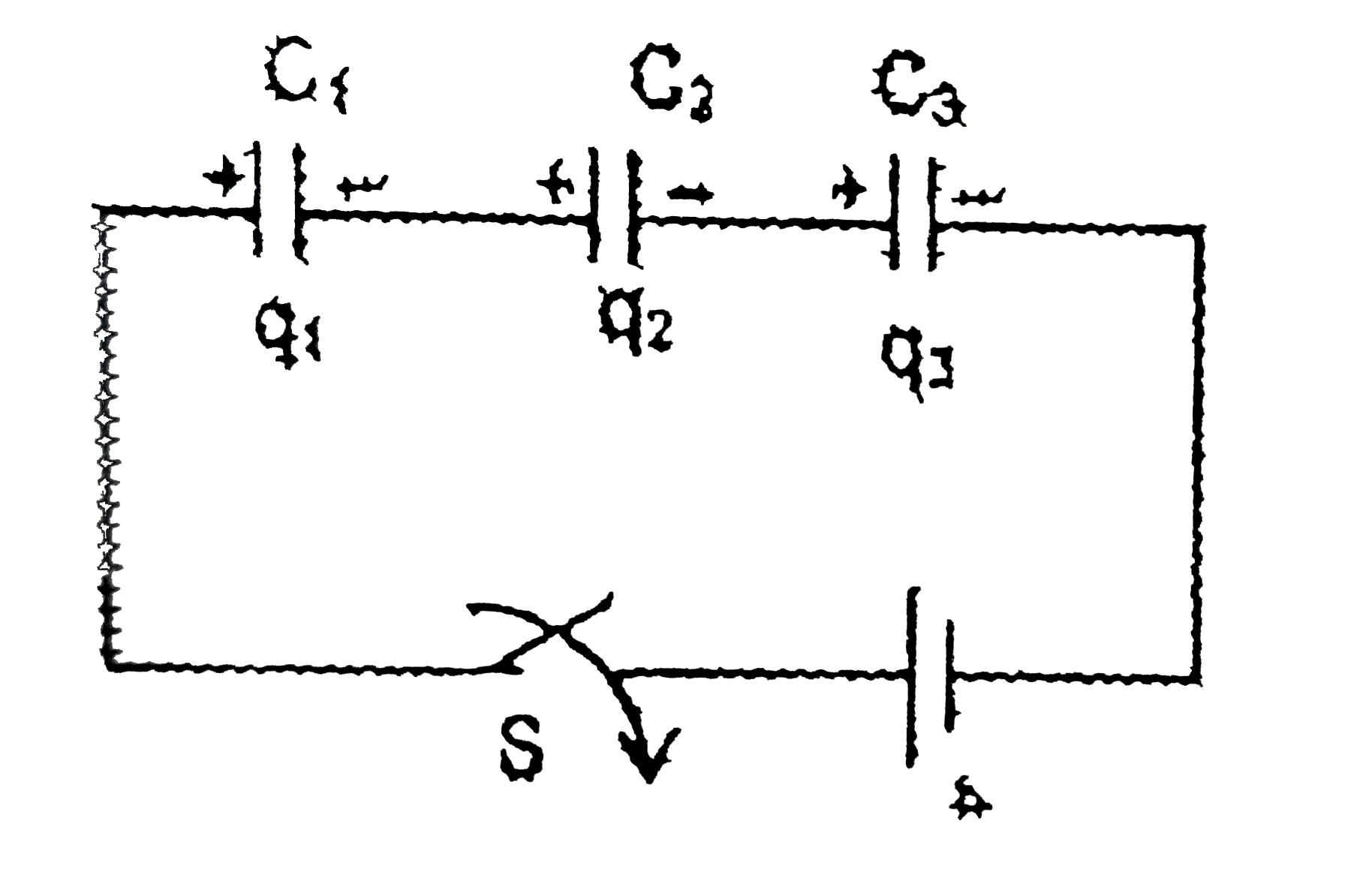
View SolutionCharges q1 , q2 and q3 are placed on capacitors of capacitance C1, C2 and C3, respectively, arranged in series as shown. Switch S is there closed. What are the final charges q'1, q'2 and q'3 on the capacitors?
Given q1=30μC, q2=μC, q3=10μC, C1=10μF, C2=20μF, C3=30μF and ε=12volt
View SolutionFind Q in the addition.
31Q+1Q3=501
View Solution
