If the resultant of three forces →F1=pˆi+3ˆj−ˆk,→F2=6ˆi−ˆkand→F3=−5ˆi+ˆj+2ˆk acting on a particle has a magnitude equal to 5 units, then the value of p is Solution in Punjabi
−6
−4
2
4
The correct Answer is:B, C
Let R be the resultant. Then
R=F1+F2+F3=(p+1)ˆi+4ˆj
Given, |R|=5. Therefore, (p+1)2+16=25.
or p+1=±3 or p=2,−4.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Statement I And Ii Type Questions)
3 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Passage Based Questions)
11 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - VECTOR ALGEBRA EXERCISES 1: Single Option Correct Type Questions
1 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
18 Videos
Similar Questions
Statement 1 : In ΔABC, −−→AB+−−→BC+−−→CA=0
Statement 2 : If −−→OA=→a,−−→OB=→b, then −−→AB=→a+→b
View SolutionLet OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel. Also, OA:CB=2:1 and OD:AB=1:3.
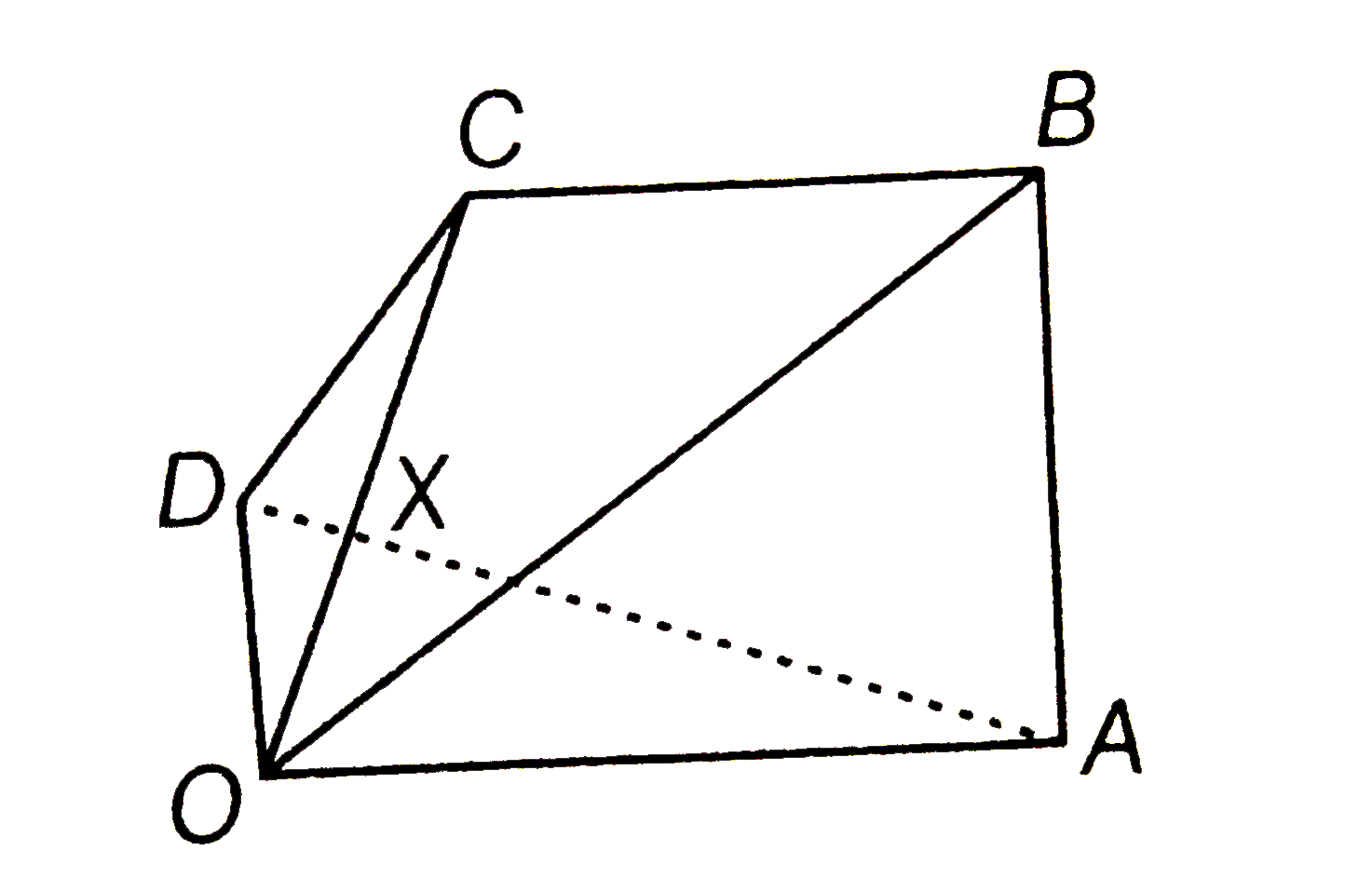
Q. The ratio AXXD is
View SolutionFind dydxify=12−x4
View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
View SolutionThe position vector of the pont where the line →r=ˆi−h∗j+ˆk+t(ˆi+ˆj−ˆk) meets plane →r.(ˆi+ˆj+ˆk)=5 is (A) 5ˆi+ˆj−ˆk (B) 5ˆi+3ˆj−3ˆk (C) 5ˆi+ˆj+ˆk (D) 4ˆi+2ˆj−2ˆk
View SolutionThree constant forces →F1=2ˆi−3ˆj+2ˆk, →F2=ˆi+ˆj−ˆk, and →F3=3ˆi+ˆj−2ˆk in newtons displace a particle from (1,−1,2) to (−1,−1,3) and then to (2,2,0) (displacement being measured in meters). Find the total work done by the forces.
View SolutionA particle acted upon by constant forces 4ˆi+ˆj−4ˆk and 3ˆi+ˆj−ˆk is displacment from the point ˆi+2ˆj+ˆk to point 5ˆi+4ˆj+ˆk.Total work done by the forces in SI unit is :
View SolutionIf the resultant of three forces →F1=pˆi+3ˆj−ˆk,→F2=−5ˆi+ˆj+2ˆkand→F3=6ˆi−ˆk acting on a particle has a magnitude equal to 5 units, then what is difference in the values of p ?
View SolutionIf the lines
ˆi−(ˆi+ˆj+ˆk)×(1−p)ˆi+3ˆj−2ˆk=0
and (→c−(3ˆi+ˆj−5ˆk))×(1−p)ˆi+3ˆj−2ˆk=0
are coplanar then the value of p is
View SolutionIf the resultant of three forces F1=pˆi+3ˆj−ˆk,F2=6ˆi−ˆkandF3=−5ˆi+ˆj+2ˆk acting on a particle has a magnitude equal to 5 units, then the value of p is
View SolutionThe volume of the parallelepiped formed by the vectors, →a=2ˆi+3ˆj−ˆk,→b=ˆi−4ˆj+2ˆk and →c=5ˆi+ˆj+ˆk is
View SolutionFollowing three forces keep a body in equilibrium. →F1=ˆi+3ˆj+2ˆk,→F2=3ˆi−4ˆk and →F3=aˆi−3ˆj+2ˆk, then the value of a is
View SolutionIf the resultant of three forces →F1=pˆi+3ˆj−ˆk,→F2=−5ˆi+ˆj+2ˆkand→F3=6ˆi−ˆk acting on a particle has a magnitude equal to 5 units, then what is difference in the values of p ?
View SolutionA particle acted upon by constant forces 4hati +hatj- 4 hatk and 3hati + hatj - hatk is displacment from the point hati+ 2hatj+ hatk to point 5hati + 4hatj +hatk .Total work done by the forces in SI unit is :
View SolutionIf the resultant of three forces →F1=pˆi−3ˆj−ˆk,→F2=−5ˆi+ˆj+2ˆkand→F3=6ˆi−ˆk acting on a particle has a magnitude equal to 5 units, then what is difference in the values of p ?
View SolutionThree constant forces →F1=2ˆi−3ˆj+2ˆk, →F2=ˆi+ˆj−ˆk, and →F3=3ˆi+ˆj−2ˆk in newtons displace a particle from (1,−1,2) to (−1,−1,3) and then to (2,2,0) (displacement being measured in meters). Find the total work done by the forces.
View Solution
