Question

If O is the circumcentre, G is the centroid and O' the orthocenter of $\Delta ABC$ prove that
(i) SA+SB+SC=3SG, where S is any point in the plane of $\Delta ABC$.
(ii) OA+OB+OC=OO'
Where, AP is diameter of the circumcircle.

Explanation

Let G be the centroid of `DeltaABC`, first we shall show that circumcentre O, orthocenter O' and centroid G are collinear and O'G=2OG.

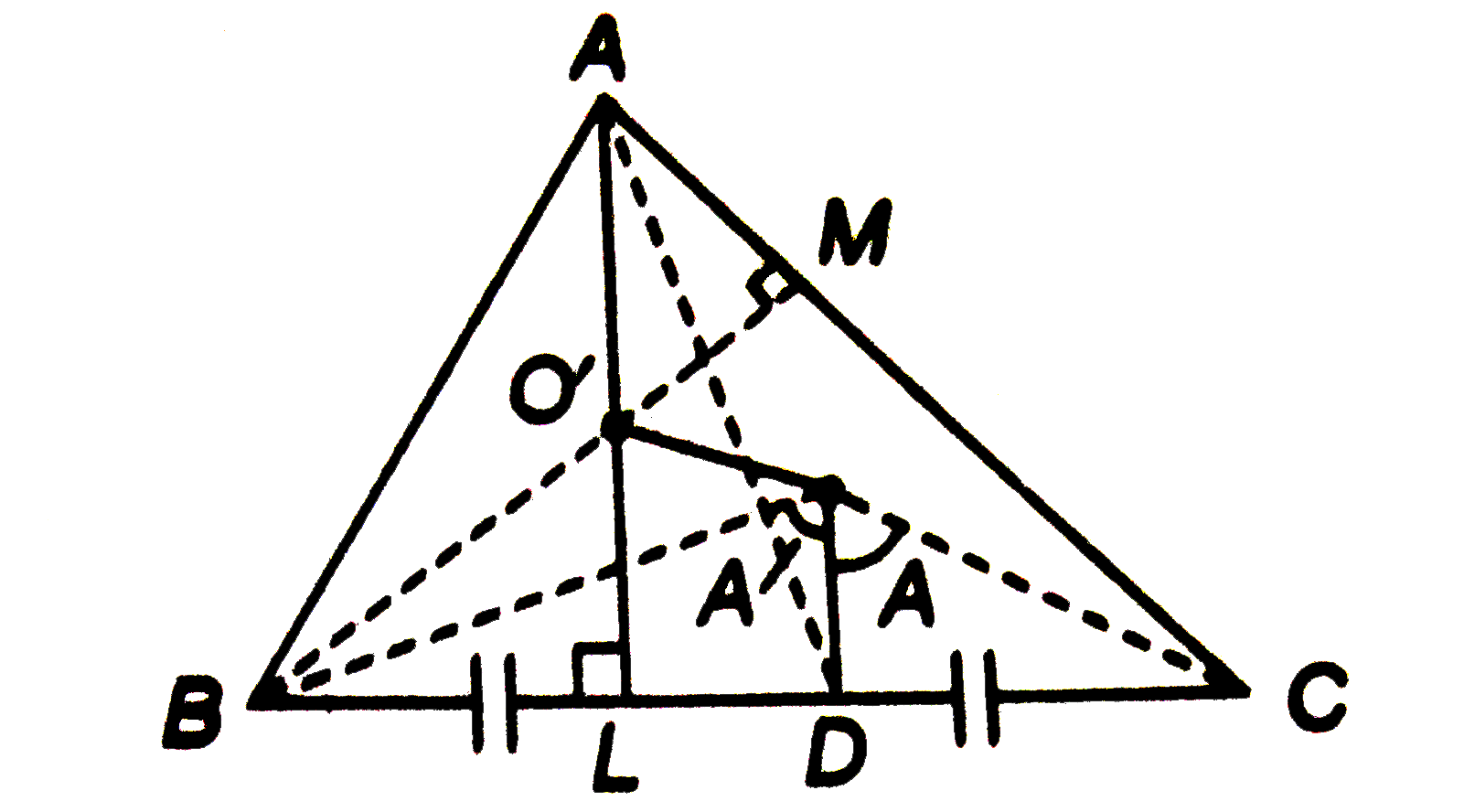
Let AL and BM be perpendiculars on the sides BC and CA, respectively. Let AD be the median and OD be the perpendicular from O on side BC. iff R is the circumradius of circumcircle of `DeltaABC`, then OB=OC=R.
In `DeltaOBD,` we have OD=R cosA . . . (i)
In `DeltaABM,AM=AB cos A=c cosA` . . . (ii)
form `DeltaAO'M,AO'=AMsec(90^(@)-C)`
=c cos A cosec C
`=(c)/(sinC)*cosA=2RcosA " "(because(a)/(sinA)=(b)/(sinB)=(c)/(sinC)=2R)`
`AO'=2(OD)` . . . (iii)
Now, `DeltaAGO' and DeltaOGD` are similar.
`therefore(OG)/(O*G)=(GD)/(GA)=(OD)/(AO')=(1)/(2)` [using Eq. (iii)]
`implies 2OG=O'G`
(i) We have, `SA+SB+SC=SA+(SB+SC)`
`=SA+2SD` (`because` D is the mid-point of BC)
`=(1+2)+SG=8SG`.
(ii) On replacing S by O in Eq. (i), we get
`OA+OB+OC=3OG`
`=2OG+OG=GO'+OG`
`=OG+GO'+O O'`.