Let O be an interior point of ΔABC such that ¯¯¯¯¯¯OA+2¯¯¯¯¯¯OB+3¯¯¯¯¯¯OC=0. Then the ratio of a ΔABC to area of ΔAOC is
The correct Answer is:3
To solve the problem, we need to find the ratio of the area of triangle ΔABC to the area of triangle ΔAOC given that ¯OA+2¯OB+3¯OC=0.
1. Understanding the Vectors:
We have the equation ¯OA+2¯OB+3¯OC=0. This means that the vector ¯OA is balanced by the weighted vectors 2¯OB and 3¯OC.
2. Setting Up the Areas:
The area of triangle ABC can be expressed in terms of the cross product of its sides. The area of triangle AOC can also be expressed similarly. We denote:
- Area of triangle ABC=12|¯ABׯAC|
- Area of triangle AOC=12|¯AOׯAC|
3. Using the Given Vector Equation:
From the vector equation, we can express ¯OA in terms of ¯OB and ¯OC:
¯OA=−2¯OB−3¯OC
4. Cross Products:
We can use the cross product to find the areas. The area of triangle AOC can be expressed as:
Area of AOC=12|¯OAׯAC|
Substituting ¯OA:
Area of AOC=12|(−2¯OB−3¯OC)ׯAC|
5. Calculating Areas:
We can expand the cross product:
Area of AOC=12(2|¯OBׯAC|+3|¯OCׯAC|)
6. Finding the Ratio:
Now, we need to find the ratio:
Area of ABCArea of AOC
Using the areas calculated, we can substitute:
12|¯ABׯAC|12(2|¯OBׯAC|+3|¯OCׯAC|)
7. Simplifying the Ratio:
After simplification, we find that:
|¯ABׯAC|2|¯OBׯAC|+3|¯OCׯAC|=3
Thus, the ratio of the area of triangle ABC to the area of triangle AOC is 3.
We have the equation ¯OA+2¯OB+3¯OC=0. This means that the vector ¯OA is balanced by the weighted vectors 2¯OB and 3¯OC.
The area of triangle ABC can be expressed in terms of the cross product of its sides. The area of triangle AOC can also be expressed similarly. We denote:
- Area of triangle ABC=12|¯ABׯAC|
- Area of triangle AOC=12|¯AOׯAC|
From the vector equation, we can express ¯OA in terms of ¯OB and ¯OC:
¯OA=−2¯OB−3¯OC
We can use the cross product to find the areas. The area of triangle AOC can be expressed as:
Area of AOC=12|¯OAׯAC|
Substituting ¯OA:
Area of AOC=12|(−2¯OB−3¯OC)ׯAC|
We can expand the cross product:
Area of AOC=12(2|¯OBׯAC|+3|¯OCׯAC|)
Now, we need to find the ratio:
Area of ABCArea of AOC
Using the areas calculated, we can substitute:
12|¯ABׯAC|12(2|¯OBׯAC|+3|¯OCׯAC|)
After simplification, we find that:
|¯ABׯAC|2|¯OBׯAC|+3|¯OCׯAC|=3
Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercises MCQ
134 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Reasoning type
8 Videos
- CONIC SECTIONSBOOK - CENGAGE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - All Questions
1344 Videos
- LIMITS AND DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - LIMITS AND DERIVATIVESEXERCISE - All Questions
691 Videos
Similar Questions
Let O be an interior point of triangle ABC, such that 2−−→OA+3−−→OB+4−−→OC=0, then the ratio of the area of ΔABC to the area of ΔAOC is
View SolutionLet O be any point in the interior of ΔABC, prove that :
AB+BC+CA<2(OA+OB+OC)
View SolutionIf ¯¯¯¯¯¯XY=3, what is the area of ΔXYZ ?
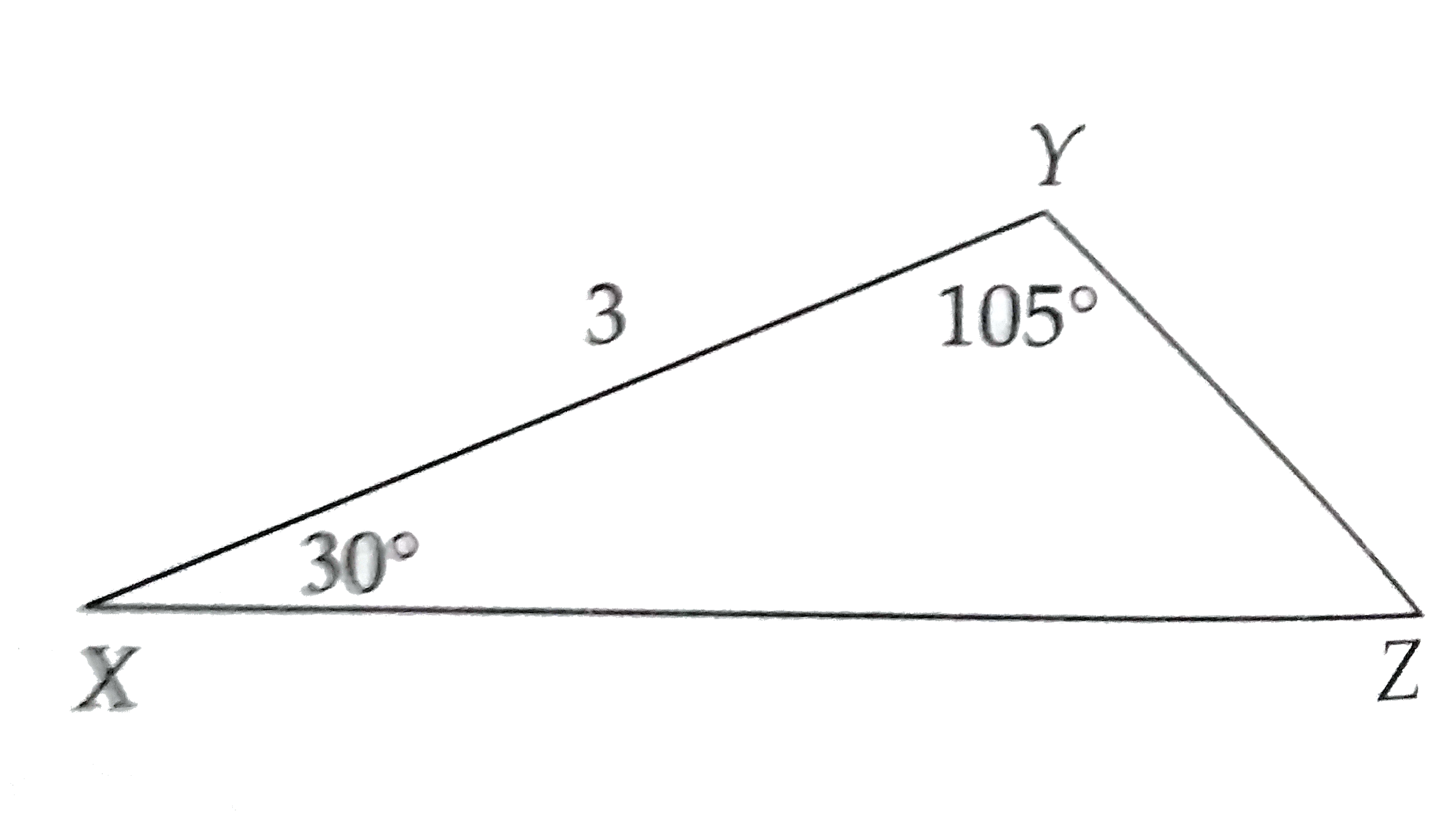
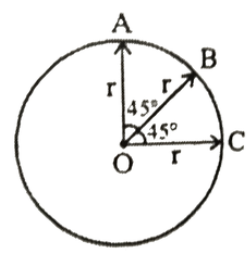
View SolutionThe resultant of the three vectors ¯¯¯¯¯¯OA,¯¯¯¯¯¯OB and ¯¯¯¯¯¯OC shown in figure :-
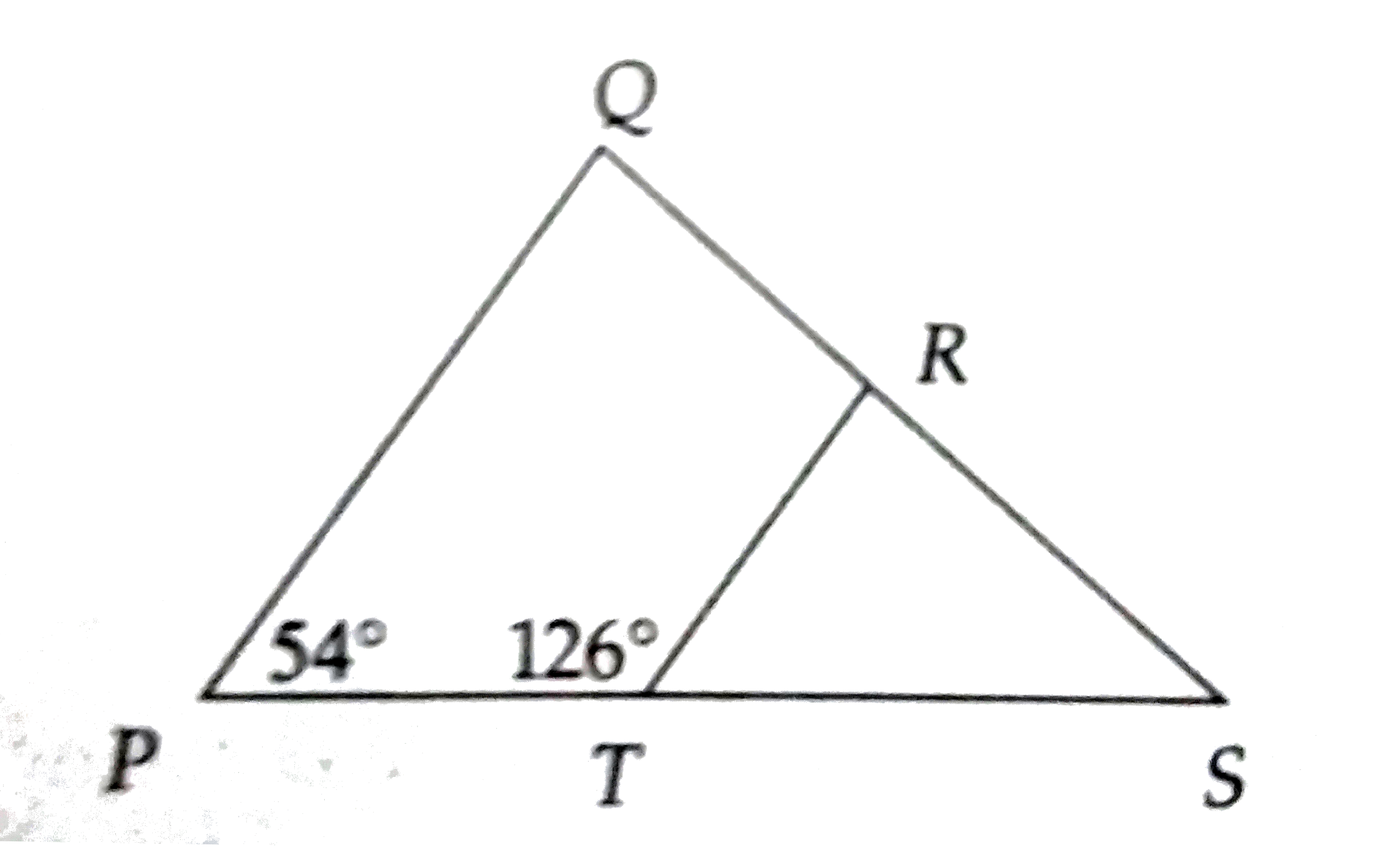
View Solution¯¯¯¯¯¯QR=¯¯¯¯¯RS. If the area of ΔRST is c2, what is the area of ΔQSP ?
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC

View SolutionIf the ratio of angles of ΔABC is 1:2:3, find the ratio of its sides.
View SolutionGiven a cube ABCD A1B1C1D1 which lower base ABCD, upper base A1B1C1D1 and the lateral edges AA1,BB1,CC1 and DD1 M and M1 are the centres of the forces ABCD and A1B1C1D1 respectively. O is a point on the line MM2 such that ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB,¯¯¯¯¯¯OC+¯¯¯¯¯¯OD=¯¯¯¯¯¯¯OM, then ¯¯¯¯¯¯¯OM=λ(OM1) is equal to
View SolutionEvaluate :
2.¯7+1.¯3
View Solution
In the figure above, the circle with center O has ¯¯¯¯¯¯PQ tangent to it at P. Find the ratio of the shaded area to the area of the circle .
View Solution
