Let A,B,C,D,E represent vertices of a regular pentangon ABCDE. Given the position vector of these vertices be a,a+b,b, $λ a$ and $λ b$ respectively.
Q. AD divides EC in the ratioSolution in Punjabi

A

$1 - cos \frac{3 π}{5} : cos \frac{3 π}{5}$

B

$1 + 2 cos \frac{2 π}{5} : cos \frac{π}{5}$

C

$1 + 2 cos \frac{π}{5} : 2 cos \frac{π}{5}$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Given ABCDE is a regular pentagon

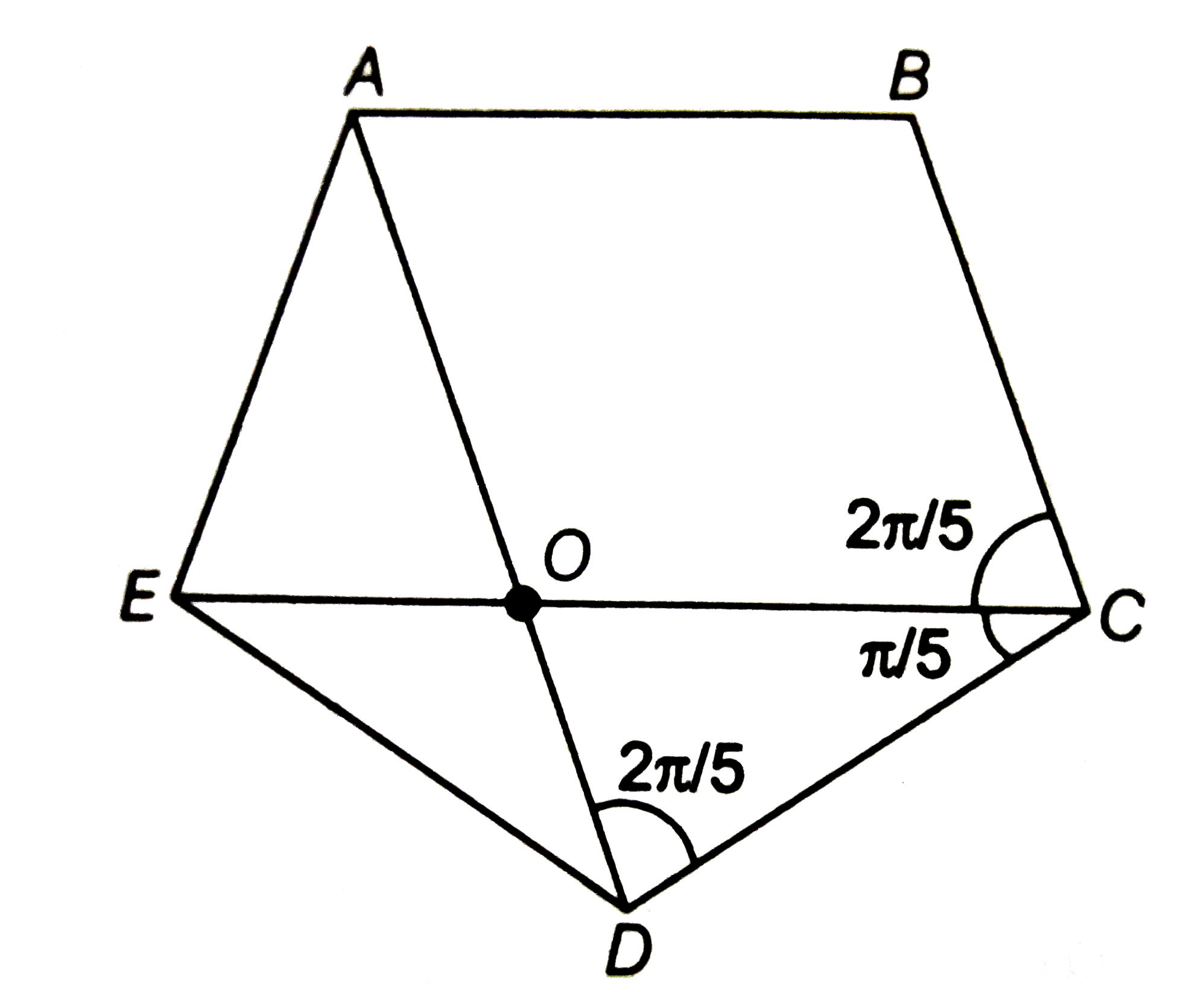
Let position vector point A and C be a and b, respectively. AD is parallel to BC and AB is parallel to EC.
Therefore,
AOCB is a parallelogram annd position vector of B is a+b.
The position vectors of E annd D are $λ b and λ a$ respectively.
Also, $O A = B C = A B = O C = 1$ (let)
therefore, $A O C B$ is rhombus.
$∠ A B C = ∠ A O C = \frac{3 π}{5}$
and $∠ O A B = ∠ B C O = π - \frac{3 π}{5} = \frac{2 π}{5}$
further, $O A = A E = 1 and O C = C D = 1$
Thus, $Δ E A O and Δ O C D$ are isosceles.
In $Δ O C D$ , using sine rule we get,
$\frac{O C}{sin \frac{2 π}{5}} = \frac{O D}{sin \frac{π}{5}}$
$\Rightarrow O D = \frac{1}{2 cos \frac{π}{5}} = O E$
$\Rightarrow A D = O A + O D = 1 + \frac{1}{2 cos \frac{π}{5}}$
$\frac{A D}{B C} = 1 + \frac{1}{2 cos \frac{π}{5}} = \frac{1 + 2 cos \frac{π}{5}}{2 cos \frac{π}{5}}$

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS-VECTOR ALGEBRA-Exercise (Questions Asked In Previous 13 Years Exam)

Home
Ask Doubt
Profile