Let A,B,C,D,E represent vertices of a regular pentangon ABCDE. Given the position vector of these vertices be a,a+b,b,λa and λb respectively.
Q. AD divides EC in the ratio
cos2π5:1
cos3π5:1
1:2cosπ5
1:2
The correct Answer is:C
Given ABCDE is a regular pentagon
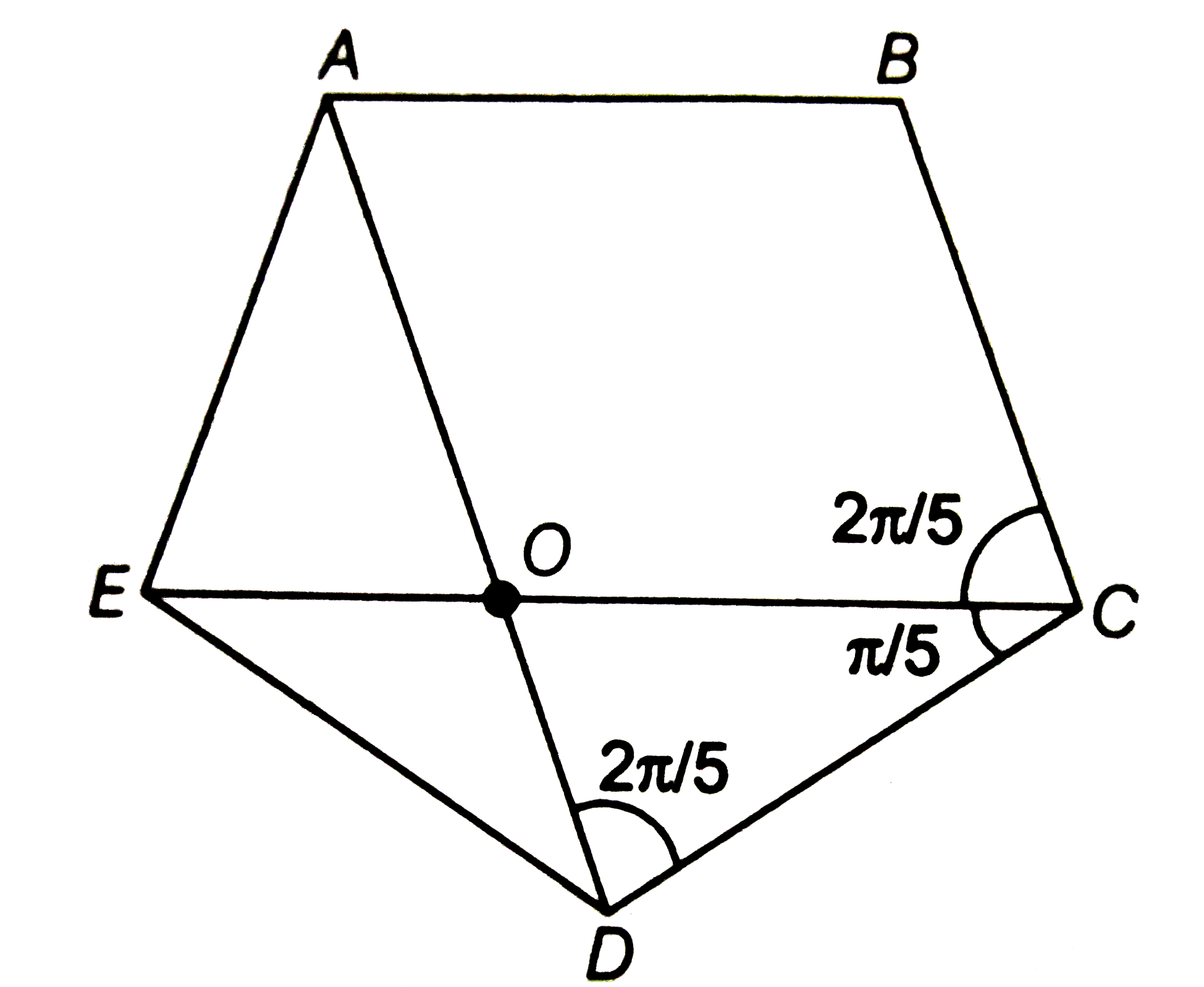
Let position vector point A and C be a and b, respectively. AD is parallel to BC and AB is parallel to EC.
Therefore,
AOCB is a parallelogram annd position vector of B is a+b.
The position vectors of E annd D are λbandλa respectively.
Also, OA=BC=AB=OC=1 (let)
therefore, AOCB is rhombus.
∠ABC=∠AOC=3π5
and ∠OAB=∠BCO=π−3π5=2π5
further, OA=AE=1andOC=CD=1
Thus, ΔEAOandΔOCD are isosceles.
In ΔOCD, using sine rule we get,
OCsin2π5=ODsinπ5
⇒OD=12cosπ5=OE
⇒AD=OA+OD=1+12cosπ5
OEOC=12cosπ5.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 1
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 2
17 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
Let A,B,C,D,E represent vertices of a regular pentagon ABCDE. Given the position vector of these vertices be →a,→a+→b,→b,λ→a and λ→b respectively. If the area of the pentagon ABCDE is k∣∣→a×→b∣∣ then k is equal to
View SolutionIf a,b,c are the position vectors of the vertices of △ABC, then area of the triangle is
View Solution
Knowledge Check
Let A, B, C, D, E represent vertices of a regular pentagon ABCDE. Given the position vector of these vertices be →a,→a+→b,→b,λ→aandλ→b, respectively.
AD divides EC in the ratioAcos2π5:1Bcos3π5:1C1:2cosπ5D1:2Let A, B, C, D, E represent vertices of a regular pentagon ABCDE. Given the position vector of these vertices be →a,→a+→b,→b,λ→aandλ→b, respectively.
The ratio ADBC is equal toA1−cos3π5:cos3π5B1+2cos2π5:cosπ5C1+2cosπ5:2cosπ5DNone of theseA, B, C, D, E, F in that order, are the vertices of a regular hexagon with centre orgin. If the position vectors of the vertices A and B are respectively, 4ˆi+3ˆj−ˆkand−3ˆi+ˆj+ˆk, then DE is equal to
A7ˆi+2ˆj−2ˆkB−7ˆi−2ˆj+2ˆkC3ˆi−ˆj−ˆkD−4ˆi−3ˆj+2ˆk
A, B, C, D, E, F in that order, are the vertices of a regular hexagon with centre orgin. If the position vectors of the vertices A and B are respectively, 4ˆi+3ˆj−ˆkand−3ˆi+ˆj+ˆk, then DE is equal to
View SolutionUnit vector perpendicular to the plane of ΔABC with position vectors a,b,c of the vertices A,B,C is
View SolutionThe position vector of four points A, B, C and D are a,b,c and d respectively . If a- b = 2(d-c) the
View SolutionThe position vector of four points A, B, C and D are a,b,c and d respectively . If a- b = 2(d-c) the
View Solutiona, b, c, d are the vertices of a square, then
View Solution
