Question

Let $A=\{x:-1\le x\le 1\}=B$ for each of the following functions from $A$ to $B$. Find whether it is surjective, injective or bijective
(i) $f\left(x\right)=\frac{x}{2}$
(ii) $g\left(x\right)=\left|x\right|$

Answer

B::C

Explanation

`A={x:-1lexle}`
`B={x:-1lexle}`
(i) `f(x)=(x)/(2)`
Let `x_(1), x_(2) inA`
`therefore f(x_(1))=f(x_(2))implies(x_(1))/(2)=(x_(2))/(2)`
`implies x_(1) = x_(2)`
`therefore` f is one-one function
Now, let `y=(x)/(2)impliesx=2y`
`implies -1leyle1`
`implies -2le2yle2implies-2lexle2`
Let `x in [-1,1]`
`therefore` There are some value of y for which x does not exist. So, f not onto.
(ii) g(x) = |x|
For x=-1, g(-1) = 1
and for x = 1, g(1) = 1
`therefore` f is not one-one function
Let y = |x|, then `y ge 0`
`therefore` f is not onto.
(iii) h(x) = x|x| = `{{:(x^(2),,xge0),(-x^(2),,xlt0):}`

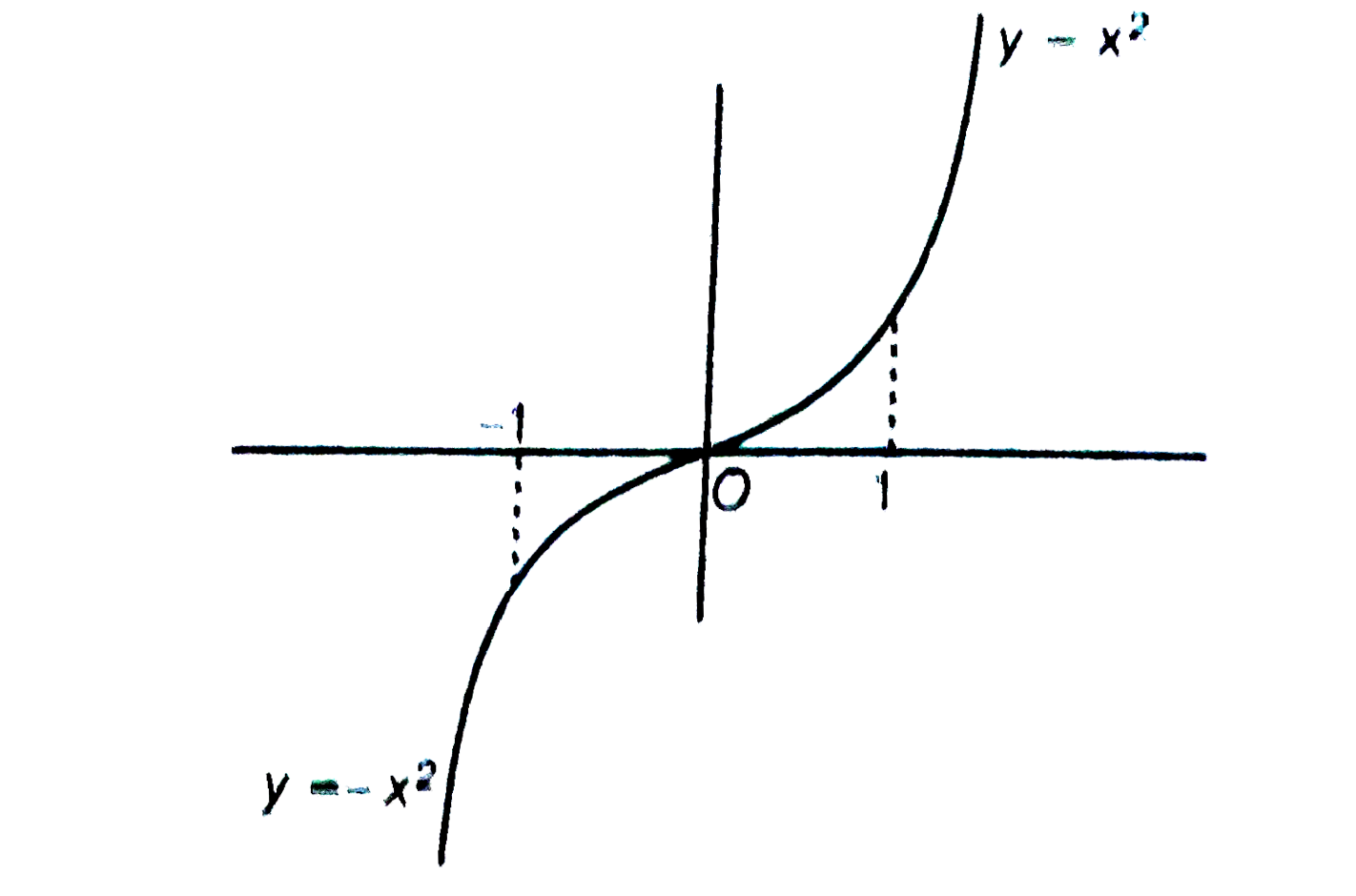
From figure, it is clear tat h is one-one and onto i.e., bijective.
(iv) `k(x) = x^(2)`

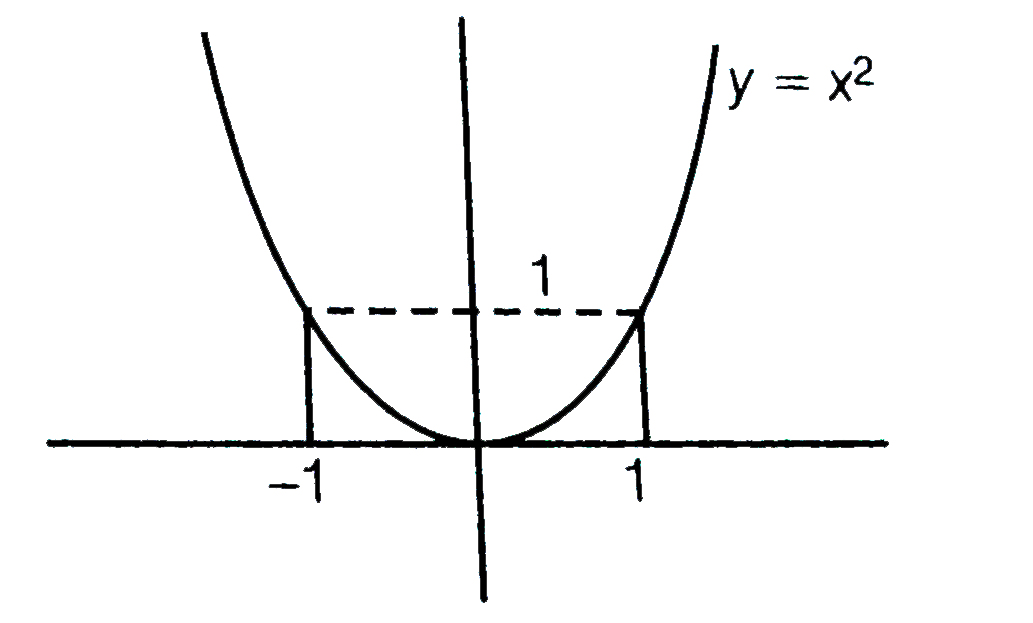
k(1) = 1
and k(-1) = 1
So, k is many-one function.
From figure, `y in (0, 1)`
`therefore` y is not onto function.
(v) `y = l(x) = sin pi x`
for x = 1, `l(1) = sin pi = 0`
for x = - 1, l(-1) = sin `(-pi)` = 0
`therefore l` is not one-one.
Now, `-1lexle1`
`implies-pilepixlepi`
`implies -1lesinpixle1`
`therefore` y is onto function.
Hence, l is surjective function.