Question

In a survey of population of 450 people, it is found that 205 can speak English, 210 can speak Hindi and 120 people can speak Tamil. If 100 people can speak both Hindi and English, 80 people can speak both English and Tamil, 35 people can speak Hindi and Tamil and 20 people can speak all the three languages, find the number of people who can speak English but not a Hindi or Tamil. Find also the number of people who can speak neither English nor Hindi nor Tamil.

Answer

45, 110

Explanation

b + e + f + g = 205 … (i)
a + d + f + g = 210 … (ii)
c + d + e + g = 120 … (iii)
f + g = 100 … (iv)
e + g = 800 … (v)
d + g = 35 … (vi)
g = 20 … (vii)

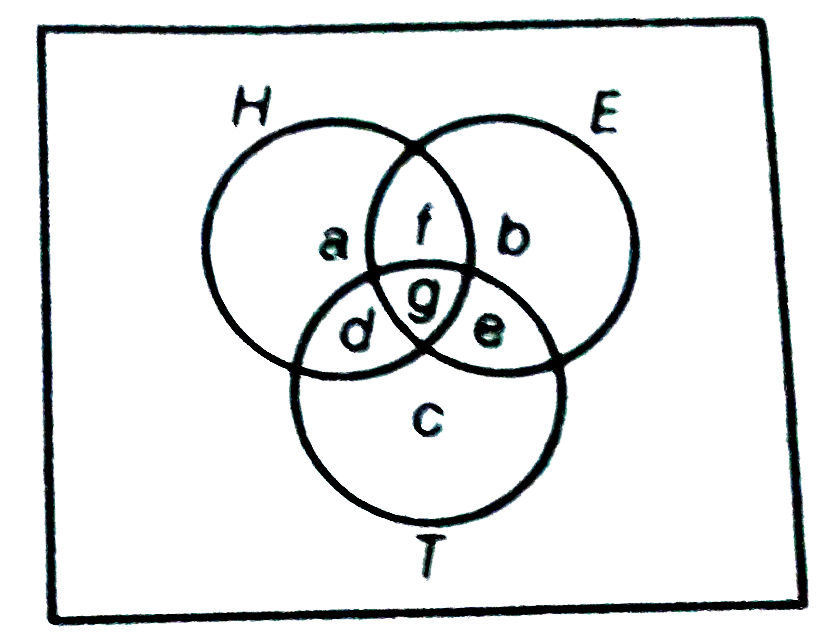
From Eqs. (vi) and (vii), d = 15
From Eqs. (vii) and (v), e = 60
From Eqs. (vii) and (iv), f = 80
From Eq. (i), b + 60 + 80 + 20 = 205 implies b = 205 - 160 implies b = 45 = Can speak English but not Hindi or Tamil. From Eq. (ii) a + 15 + 80 + 20 = 210
`implies a + 115 = 210 implies a = 95`
From Eq. (iii), c + 15 + 60 + 20 = 120
implies c = 120 - 95 implies c = 25
People who can speak neither E nor H nor T
= 450 - (95 + 45 + 25 + 15 + 60 + 80 + 20)
= 450 - 340 = 110