Let x2−(m−3)x+m=0(mεR) be a quadratic equation . Find the values of m for which the roots are real and distinct Solution in Punjabi

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Let f(x)=x2−(m−3)x+m
Here a=1,b=−(m−3),c=m
and D=b2−4ac=(m−3)2−4m
=m2−10m+9=(m−1)(m−9)
and x-x coordinate of vertex =−b2a=(m−3)2
(i) Both the roots are smaller than 2 D≥0
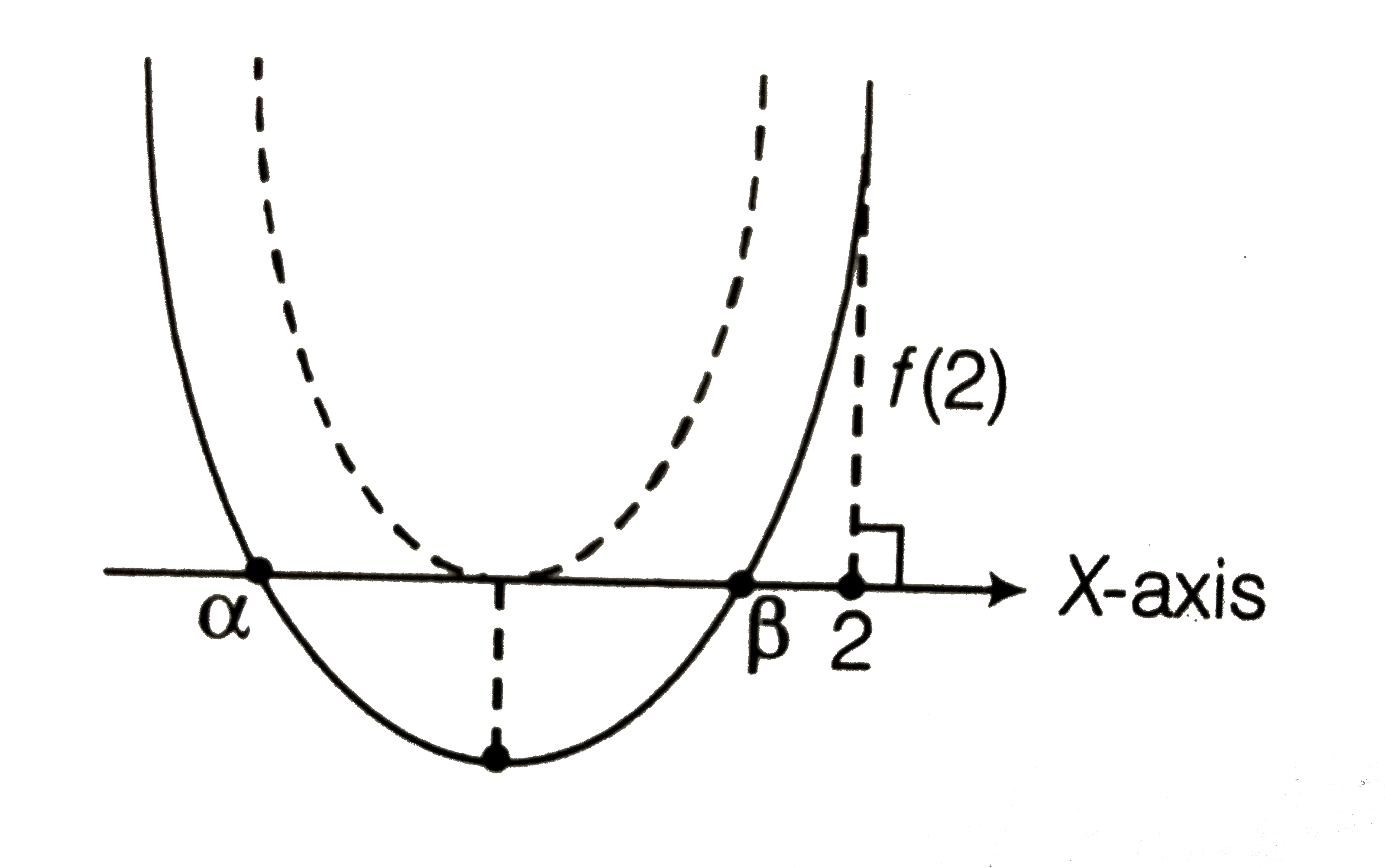
ocr_image
i.e. (m−1)(m−9)≥0
∴mε(−∞1[∪[9,∞) ............i
f(2)>0
i.e. 4−2(m−3)+m≥0
⇒m<10
∴mε(−∞,10)......ii and x- coordinate of vertex <2
i.e. (m−3)2<⇒m<7
∴mε(−∞,7) iii
On combining Eqs.i,ii, and iii we get
mε(−∞,1]
(ii) Both the roots are greater than 2 D≥0
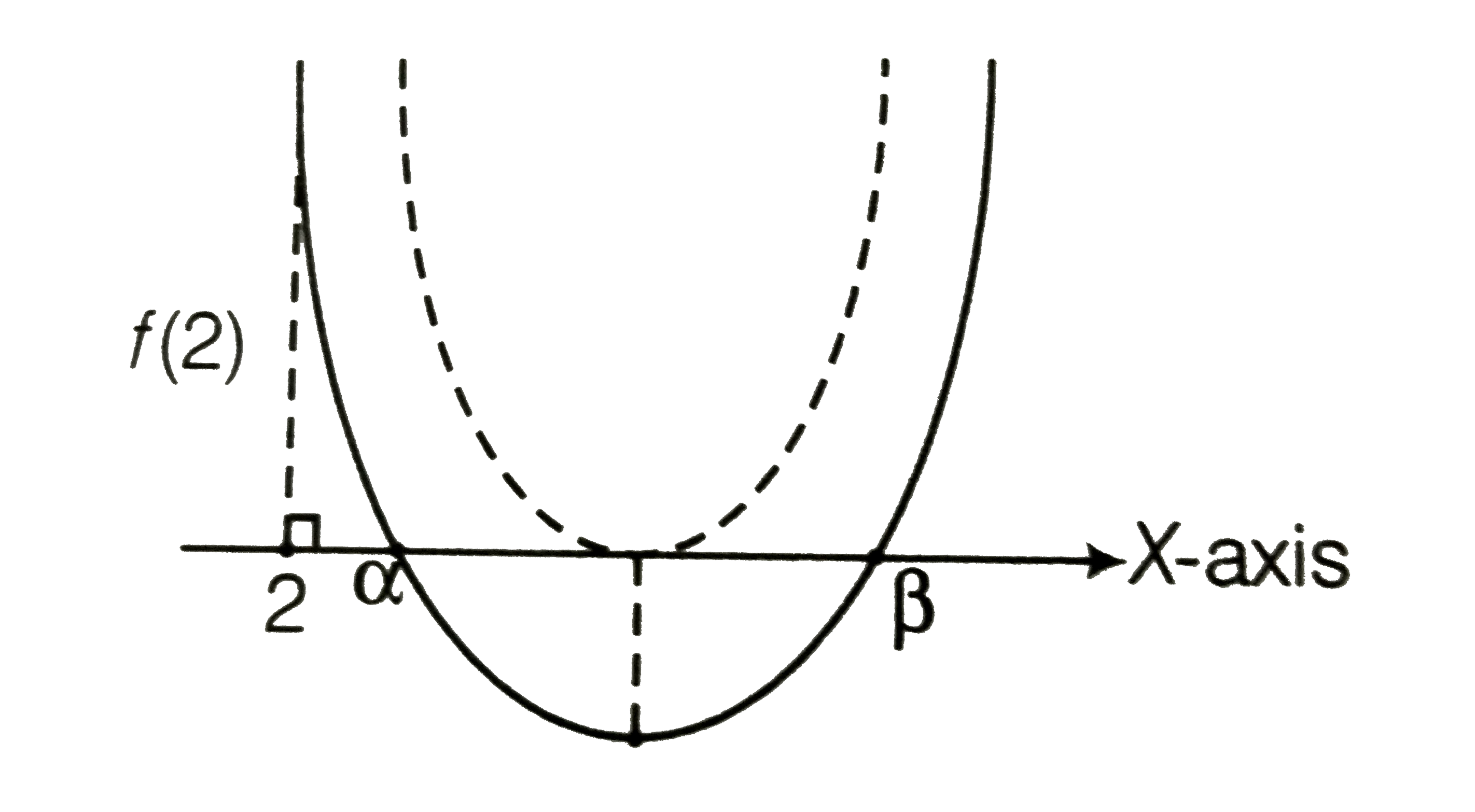
ocr_image
i.e. (m−1)(m−9)≥0
∴mε(−∞,1]ε[9,∞).........i
f(2)>0
i.e. 4−2(m−3)+m>0
⇒m<10......ii
and x-coordinate of vertex >2
i.e. (m−3)2>⇒m<7
∴mε(7,∞) .....iii
On combining Eqs. i, ii and iii we get
mε[9,10)
(iii) One root is smaller than 2 and the other root is greater than 2
D<0
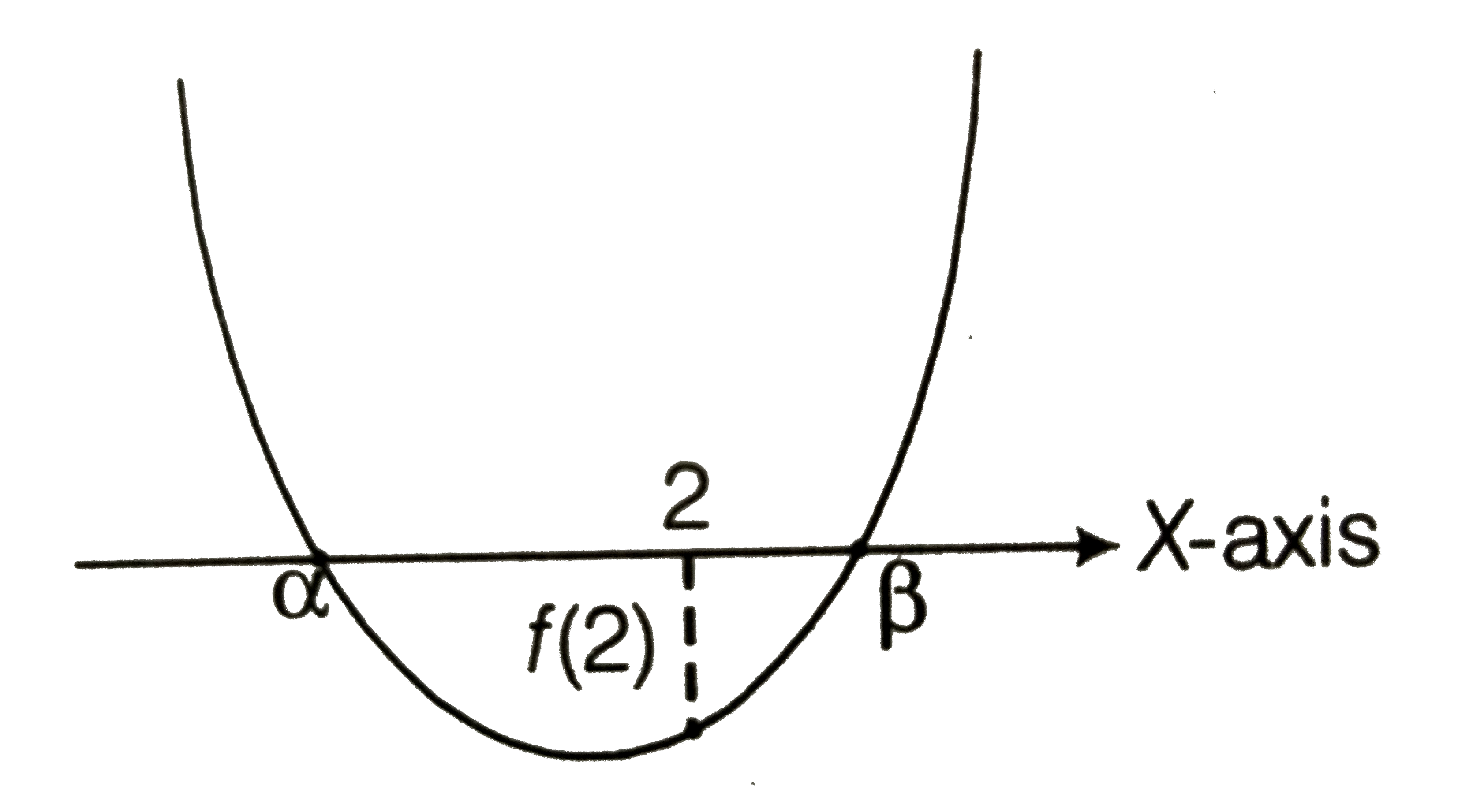
ocr_image
i.e. (m−1)(m−9)>0
∴mε(−∞,1)∪(9,∞)....i
f(2)<0
i.e 4−2(m−3)+m<0
∴m>10
∴mε(10,∞)....ii
On combining Eqs i and ii we get
mε(10,∞)
(iv) Exactly one root lies in the interval (1,2)
D>0
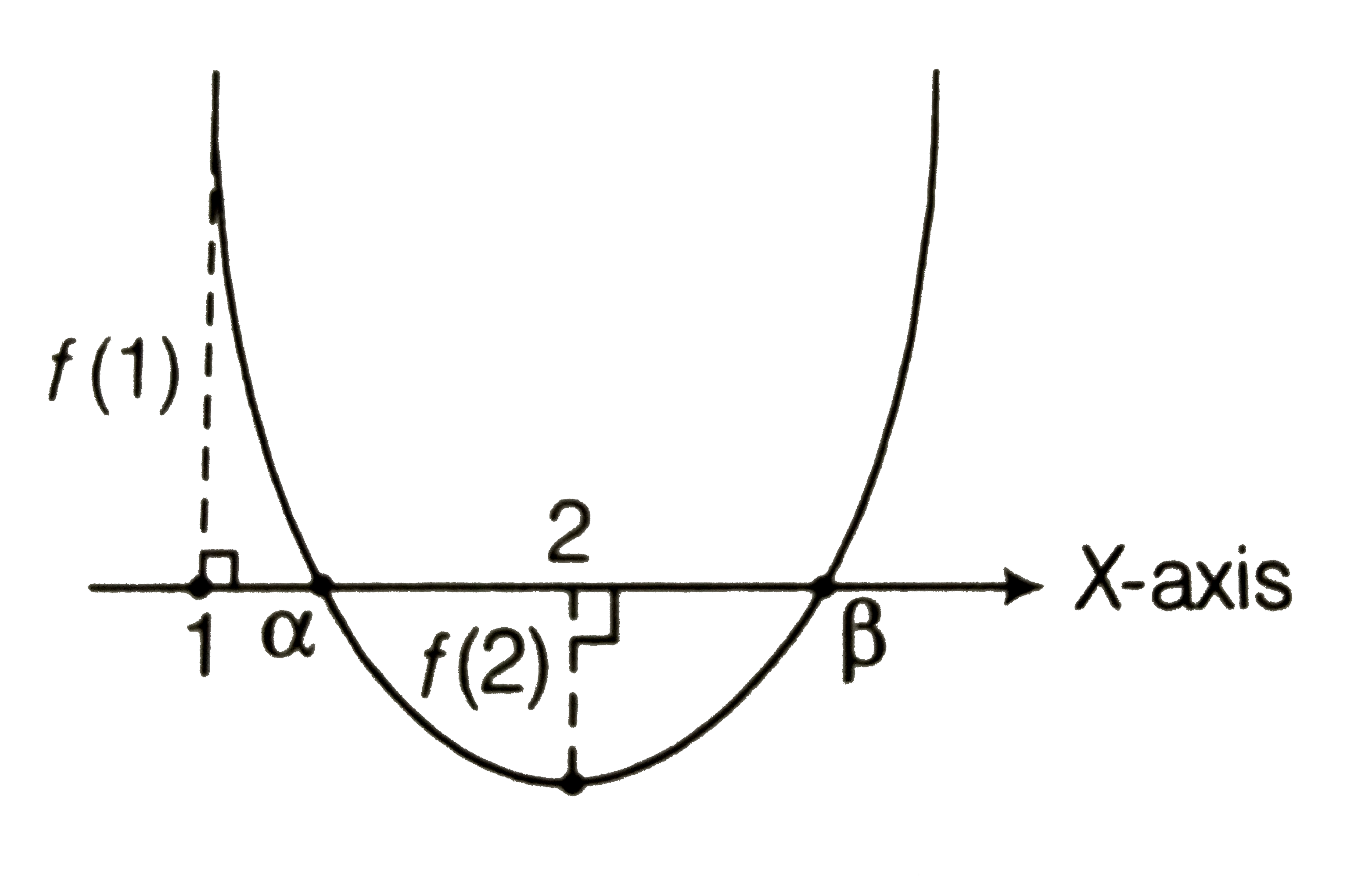
ocr_image
i.e., (m−1)(m−9)>0
∴mε(−∞,1)∪(9,∞)...i
f(1)f(2)<0
(1−(m−3)+m)(4−2(m−3)+m)<0
⇒4(−m+10)<0
⇒m−10>0⇒m>10
∴mε(10,∞) ....ii
On combining Eqs (i) and (ii) we get
mε(10,∞)
(v) Both the roots lie in the interval (1,2)
D≥0
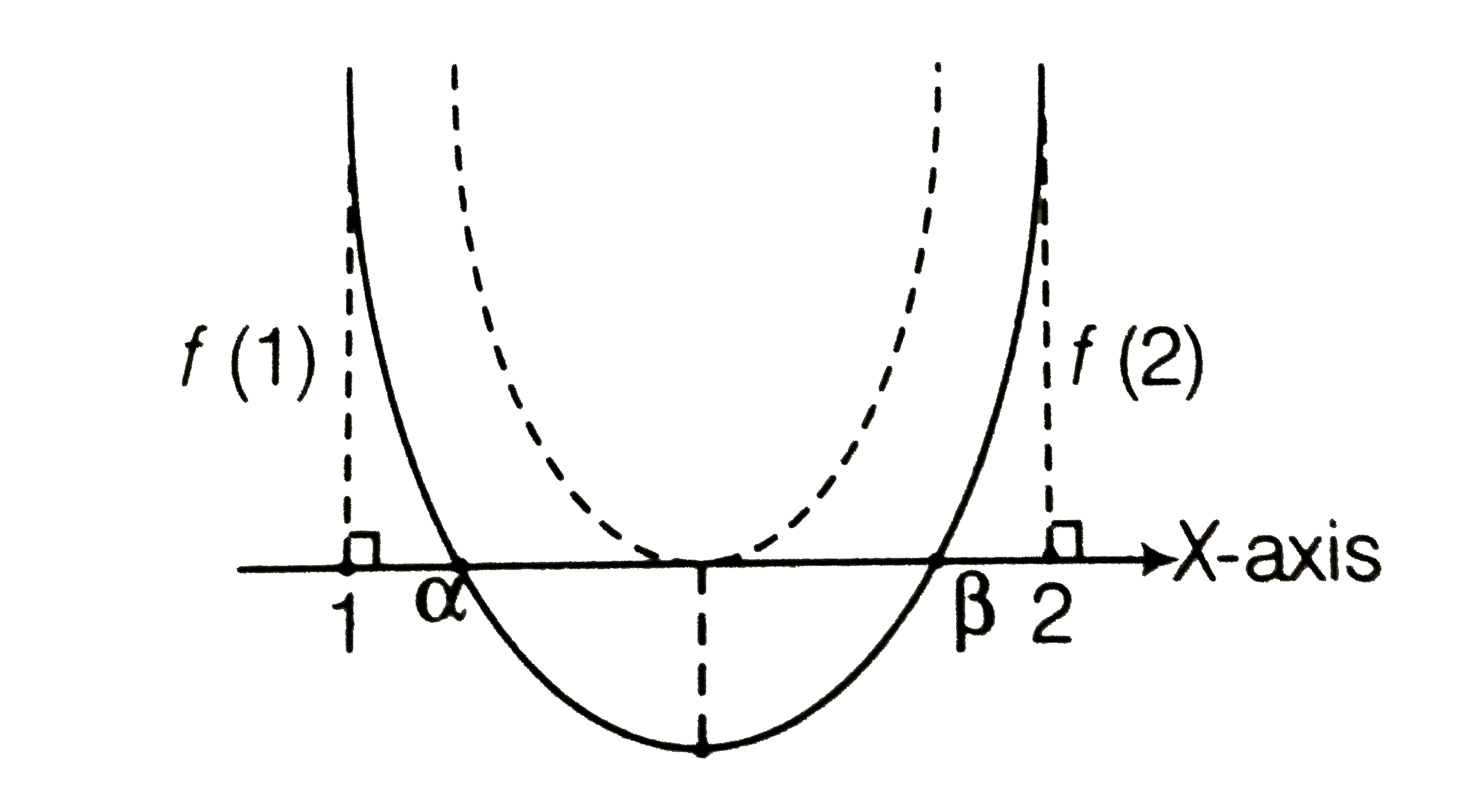
ocr_image
i.e. (m−1)(m−9)≥0
∴mε(−∞,1]∪[9,∞)...i
f(1)>0
i.e. (1−(m−3)+m)>0⇒4>0
∴mεR.ii
f(2)>0
i.e. 4−2(m−3)+m>0⇒m<10
∴mε(−∞,10)..iii
1<x coordinate of vertex <2
i.e. 1<(m−3)2<2
⇒2<m−3<4 or 5<m<7
∴mε(5,7).iv
On combining Eqs. i,ii,iii and iv we get
mεϕ
(vi) One root is greater than 2 and the other root is smaller than 1D>0
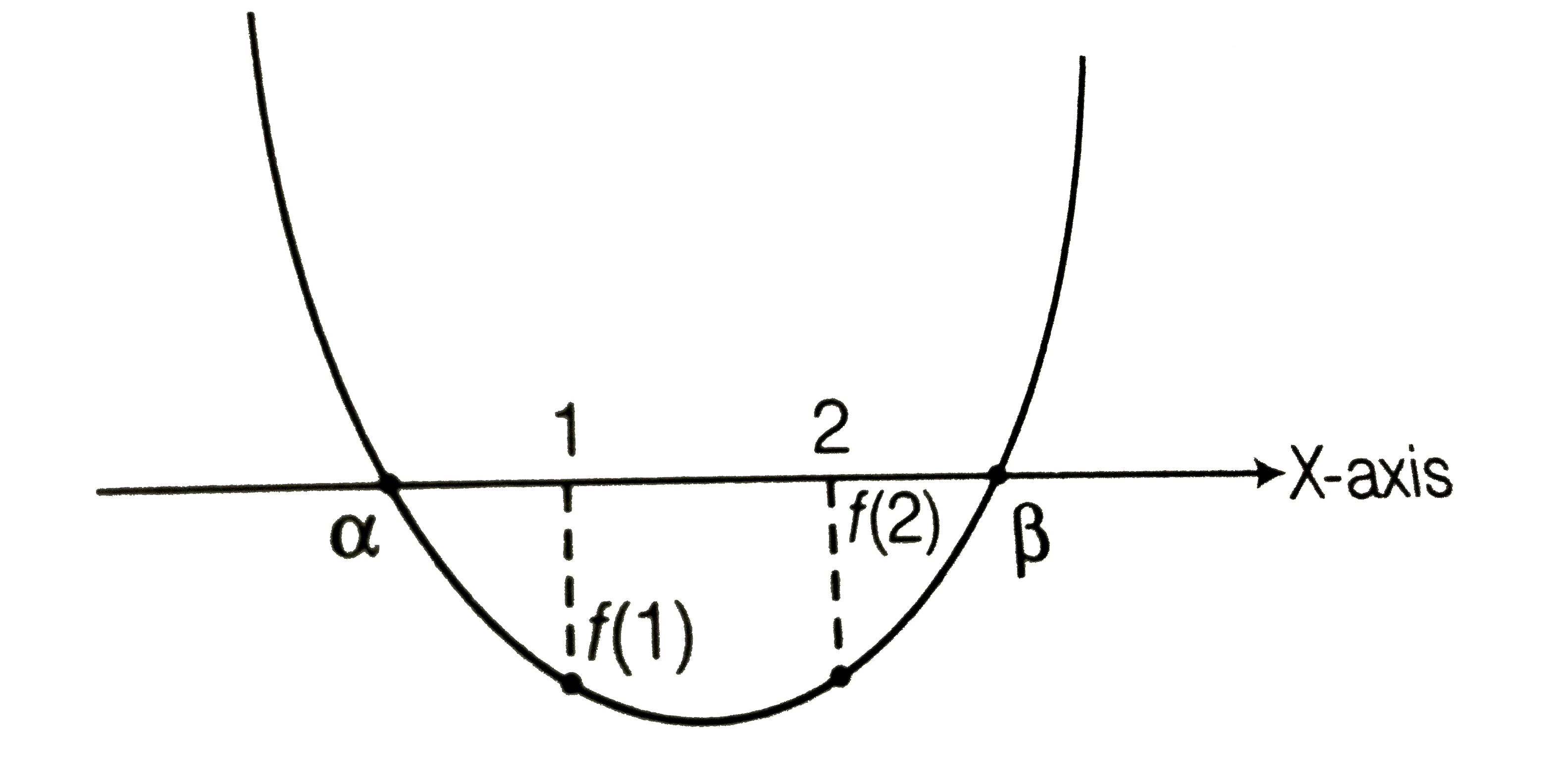
ocr_image
i.e. (m−1)(m−9)>0
∴mε(−∞,1)∪(9,∞).i
f(1)<0
i.e. 4<0 which is not possible.
Thus , no such m exists.
(vii) At least one root lie in the interval (1,2)
Case I Exactly one root lies in (1,2)
mε(10,∞) [from (iv) part]
Case II Both roots lie in the interval (1,2).
mε(10,∞)
(viii) Atleast one root is greater than 2
Case I One root is smaller than 2 and the other root is greater than 2.
Then, mε(10,∞) [from iii) part]
Case II Both the roots are greaters than 2 then mε[9,10).
Hence atleast one root is greater than 2.
∴mε(10,∞)∪[9,10) or mε[9,10)∪(10,∞)

Updated on:21/07/2023
|
Class 12MATHSQUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions