Find the valuesof m for which exactly one root of the equation x2−2mx+m2−1=0 lies in the interval (−2,4)Solution in Punjabi
Let f(x)=x2−2mx+x2−1, as exactly one root of f(x)=0 lies in the interval (−2,4), we can take D>0 and f(−2)f(4)<0.
(i) Consider D>0
(−2m)2−4.1(m2−1)>0⇒4>0
∴mεR……………i
(ii) Consider f(−2)f(4)<0
(4+4m+m2−1)(16−8m+m2−1)<0
⇒(m92)+4m+3)(m2−8m+15)<0
⇒(m+1)(m+3)(m−3)(m−5)<0
⇒(m+3)(m+1)(m−3)(m−5)<0
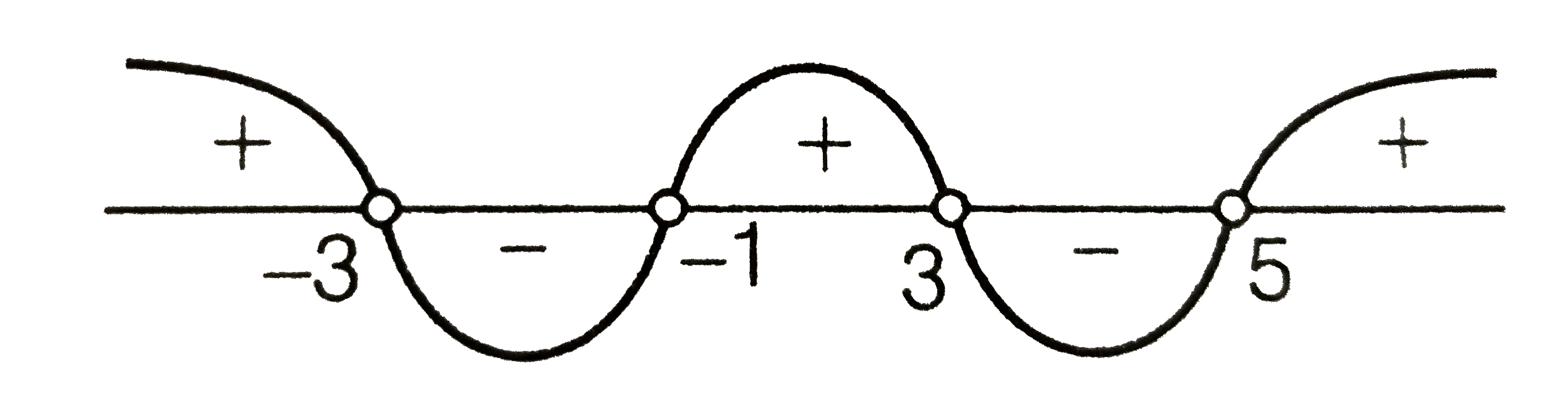
∴mε(−3,−1)∪(3,5).........ii
Hence the values fo m satisfying Eq. (i) and (ii) at the same time are mε(−3,−1)∪(3,5).
Related Playlists
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 111videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 210videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)1videos
THE STRAIGHT LINES
- BOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam2videos
THREE DIMENSIONAL COORDINATE SYSTEM
Similar Questions
If (a2−1)x2+(a−1)x+a2−4a+3=0 is identity in x , then find the value of a .
03:48View SolutionIf α and β are the roots of the equation 2x2−3x+4=0, then the equation whose roots are α2 and β2, is a. 4x2+7x+16=0 b. 4x2+7x+6=0 c. 4x2+7x+1=0 d. 4x2−7x+16=0
03:15View SolutionSolve the following system of inequalities graphically
x+5y≤25,2x+2y≥2,2x−2y≤0,x≥0,y≥002:45View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
07:20View Solutionfind the set of value of m for which exactly one root of the equation x^(2)+mx+m^(2)+6m=0 lie in the interval (-2,0)
07:24View Solutionfind all the possible values of k for which exactly one root of the quadratic equation x^(2)-(6k-1)-2k=0 lies in the interval :
01:46View Solutionif the roots of the quadratic equation (4p−p2−5)x2 −2mx+m2−1=0 are greater then - 2 less then 4 lie in the interval
02:46View SolutionIf exactly one root of the quadratic equation x2−(a+1)+2a=0 lies in the interval (0,3) then the set of value 'a' is given by :
01:42View SolutionIf number of integeral values of 'm' for which exactly one root of the equation. x2+3mx+m2−4=0 lies on the interval (−6,2) is k. Then [k5] = (where [.] denote greatest integer function).
02:53View Solutionif the roots of the quadratic equation (4p−p2−5)x2 −2mx+m2−1=0 are greater then - 2 less then 4 lie in the interval
13:18View Solutionm के वह सभी मान, जिसके लिये समीकरण x2−2mx+m2−1=0 के दोनों मूल -2 से बड़े परन्तु 4 से कम हो, निम्न में से किस अन्तराल में स्थित है:
(i) m>3 (ii) −1<m<3 (iii) 1<m<4 (iv) −2<m<005:25View SolutionFind the values of x for the given equation 3x2+5x−2=0
10:08View SolutionIf x=2 and x=3 are roots of the equation 3x2−2mx+2n=0, find the values of m and n.
08:19View SolutionLet x2−(m−3)x+m=0(mεR) be a quadratic equation . Find the values of m for which the roots are (ix)one root is smaller than 2 & other root is greater than 2 (x) both the roots are greater than 2 (xi) both the roots are smaller than 2 (xii)exactly one root lies in the interval (1;2) (xiii) both the roots lies in the interval (1;2) (xiv) atleast one root lies in the interval (1;2) (xv) one root is greater than 2 and the other root is smaller than 1
02:24View Solutionf(x)=x2−(m−3)x+m=0 is a quadratic equation, find values of m for which
exactly one root lies in the interval [2,3]11:10View SolutionFind the values of the parameter a for which the roots of the quadratic equation x^2+2(a-1)x+a+5=0 are such that exactly one root lies in the interval (1,3)
04:27View Solution

