Area of triangle having angular points
$A [a m_{1} m_{2}, (m_{1} + m_{2})], B [a m_{2} m_{3}, a (m_{2} + m_{3})$ and $C [a m_{3} m_{1} . a (m_{3} + m_{1})]$ is

A

$(m_{1} - m_{2}) (m_{2} - m_{3}) (m_{3} - m_{1})$

B

$a^{2} (m_{1} - m_{2}) (m_{2} - m_{3}) (m_{3} - m_{1})$

C

$\frac{1}{2} a^{2} (m_{1} - m_{2}) (m_{2} - m_{3}) (m_{3} - m_{1})$

D

none of these

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:C

To find the area of the triangle with vertices A, B, and C given by the coordinates:
- A $(a m_{1} m_{2}, (m_{1} + m_{2}))$
- B $(a m_{2} m_{3}, a (m_{2} + m_{3}))$
- C $(a m_{3} m_{1}, a (m_{3} + m_{1}))$
we will use the formula for the area of a triangle given by its vertices $(x_{1}, y_{1})$ , $(x_{2}, y_{2})$ , and $(x_{3}, y_{3})$ :
$Area = \frac{1}{2} | x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2}) |$
1. Identify the Coordinates:
- Let $A = (x_{1}, y_{1}) = (a m_{1} m_{2}, m_{1} + m_{2})$
- Let $B = (x_{2}, y_{2}) = (a m_{2} m_{3}, a (m_{2} + m_{3}))$
- Let $C = (x_{3}, y_{3}) = (a m_{3} m_{1}, a (m_{3} + m_{1}))$
2. Substitute the Coordinates into the Area Formula:
$Area = \frac{1}{2} | a m_{1} m_{2} (a (m_{2} + m_{3}) - a (m_{3} + m_{1})) + a m_{2} m_{3} (a (m_{3} + m_{1}) - (m_{1} + m_{2})) + a m_{3} m_{1} ((m_{1} + m_{2}) - a (m_{2} + m_{3})) |$
3. Simplify Each Term:
- For the first term:
$a m_{1} m_{2} (a (m_{2} + m_{3}) - a (m_{3} + m_{1})) = a m_{1} m_{2} (a (m_{2} - m_{1}))$
- For the second term:
$a m_{2} m_{3} (a (m_{3} + m_{1}) - (m_{1} + m_{2})) = a m_{2} m_{3} (a (m_{3} - m_{2}))$
- For the third term:
$a m_{3} m_{1} ((m_{1} + m_{2}) - a (m_{2} + m_{3})) = a m_{3} m_{1} (m_{1} + m_{2} - a (m_{2} + m_{3}))$
4. Combine the Terms:
$Area = \frac{1}{2} | a (m_{1} m_{2} (m_{2} - m_{1}) + m_{2} m_{3} (m_{3} - m_{2}) + m_{3} m_{1} (m_{1} + m_{2} - a (m_{2} + m_{3}))) |$
5. Factor Out Common Terms:
- Factor out $a$ from the expression to simplify:
$Area = \frac{a}{2} | m_{1} m_{2} (m_{2} - m_{1}) + m_{2} m_{3} (m_{3} - m_{2}) + m_{3} m_{1} (m_{1} + m_{2} - a (m_{2} + m_{3})) |$
6. Final Expression for Area:
- The final expression for the area of the triangle is:
$Area = \frac{a}{2} | m_{1} m_{2} (m_{2} - m_{1}) + m_{2} m_{3} (m_{3} - m_{2}) + m_{3} m_{1} (m_{1} + m_{2} - a (m_{2} + m_{3})) |$

Updated on:7/8/2024

|

Class 10 MATHS COORDINATE GEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

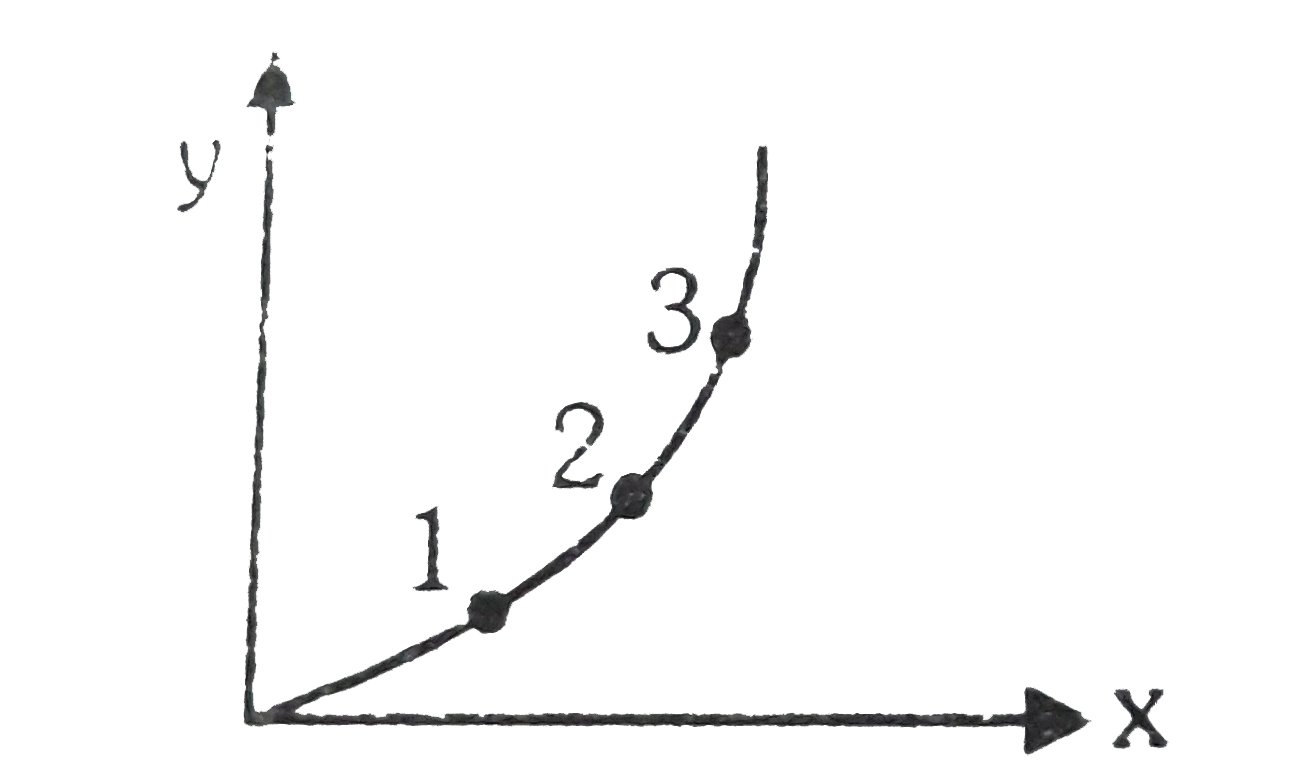
The slope of graph as shown in figure at points 1, 2 and 3 is $m_{1}, m_{2} and m_{3}$ respectively then

A $m_{1} > m_{2} > m_{3}$
B $m_{1} < m_{2} < m_{3}$
C $m_{1} = m_{2} = m_{3}$
D $m_{1} = m_{3} > m_{2}$

CENGAGE-AREA OF A TRIANGLE -TEST YOURSELF (LEVEL 3 )

Home
Ask Doubt
Profile