The fluid cortained in a bucket can fill four large bottles or seven small bottles. A full large bottle is ussed to fill an empty small bottle. What fraction of the fluid is left over in the large battle when the small one is full ?
27
37
47
57
The correct Answer is:C
To solve the problem step by step, we will follow these instructions:
1. Define the Capacity of the Bucket:
Let the total capacity of the bucket be x liters.
2. Determine the Capacity of One Large Bottle:
Since the bucket can fill 4 large bottles, the capacity of one large bottle is:
Capacity of one large bottle=x4
3. Determine the Capacity of One Small Bottle:
Since the bucket can fill 7 small bottles, the capacity of one small bottle is:
Capacity of one small bottle=x7
4. Calculate the Fluid Used to Fill the Small Bottle:
When a full large bottle is used to fill an empty small bottle, the amount of fluid transferred is equal to the capacity of one large bottle:
Fluid used=x4
5. Calculate the Remaining Fluid in the Large Bottle:
To find out how much fluid is left in the large bottle after filling the small bottle, we subtract the capacity of the small bottle from the capacity of the large bottle:
Remaining fluid=x4−x7
6. Find a Common Denominator:
The least common multiple (LCM) of 4 and 7 is 28. We will convert both fractions to have a common denominator:
x4=7x28andx7=4x28
7. Subtract the Two Fractions:
Now we can subtract the two fractions:
Remaining fluid=7x28−4x28=3x28
8. Calculate the Fraction of Fluid Left in the Large Bottle:
To find the fraction of the fluid left in the large bottle, we divide the remaining fluid by the total capacity of the large bottle:
Fraction left=Remaining fluidCapacity of one large bottle=3x28x4
9. Simplify the Fraction:
When we simplify this, we have:
Fraction left=3x28×4x=3⋅428=1228=37
10. Final Answer:
Thus, the fraction of the fluid left over in the large bottle when the small one is full is:
37
Let the total capacity of the bucket be x liters.
Since the bucket can fill 4 large bottles, the capacity of one large bottle is:
Capacity of one large bottle=x4
Since the bucket can fill 7 small bottles, the capacity of one small bottle is:
Capacity of one small bottle=x7
When a full large bottle is used to fill an empty small bottle, the amount of fluid transferred is equal to the capacity of one large bottle:
Fluid used=x4
To find out how much fluid is left in the large bottle after filling the small bottle, we subtract the capacity of the small bottle from the capacity of the large bottle:
Remaining fluid=x4−x7
The least common multiple (LCM) of 4 and 7 is 28. We will convert both fractions to have a common denominator:
x4=7x28andx7=4x28
Now we can subtract the two fractions:
Remaining fluid=7x28−4x28=3x28
To find the fraction of the fluid left in the large bottle, we divide the remaining fluid by the total capacity of the large bottle:
Fraction left=Remaining fluidCapacity of one large bottle=3x28x4
When we simplify this, we have:
Fraction left=3x28×4x=3⋅428=1228=37
Thus, the fraction of the fluid left over in the large bottle when the small one is full is:
37
Topper's Solved these Questions
- FRACTIONS AND DECIMALSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - FRACTIONS AND DECIMALSEXERCISE - QUESTIONS BANK
30 Videos
- FRACTIONS AND DECIMALSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - FRACTIONS AND DECIMALSEXERCISE - SELF ASSESSEMENT SHEET
10 Videos
- FACTORIZATION OF ALGEBRAIC EXPRESSIONS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - FACTORIZATION OF ALGEBRAIC EXPRESSIONS EXERCISE - SELF ASSESSMENT SHEET-8
10 Videos
- HCF AND LCMBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - HCF AND LCMEXERCISE - SELF ASSESSMENT SHEET-3
10 Videos
Similar Questions
The fluid contained in a bucket can fill four large bottles or seven small bottles. A full large bottle is used to fill an empty small bottle. What fraction of the fluid is left over in the large bottle when the small one is full? 27 (b) 37 (c) 47 (d) 57
View Solution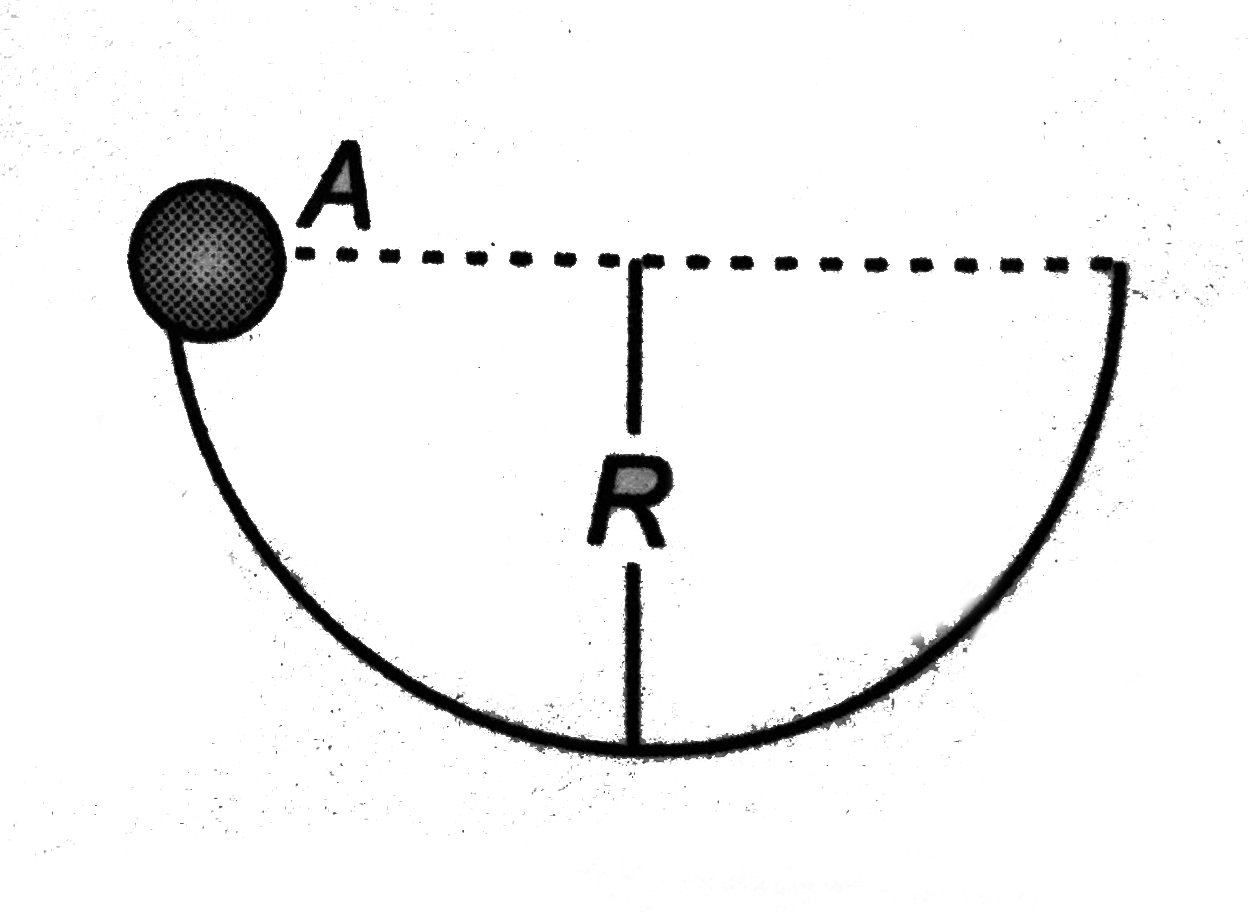
A small solid cylinder of radius r is released coaxially from point A inside the fixed large cylindrical bawl of radius R as shown in figure. If the friction between the small and the large cylinder is sufficient enough to prevent any slipping then find.
(a). What fractions of the total energy are translational and rotational when the small cylinder reaches the bottom of the larger one?
(b). The normal force exerted by the small cylinder on the larger one when it is at the bottom.
View Solution
Knowledge Check
Three bottles of equal capacity are containing a mixture of milk and water in ratio 2: 1, 3:7 and 4: 11 respectively. These three bottles are emptied into a large bottle. What is the ratio of milk and water respectively in this large bottle?
A37:53B37:90C37:30D7:30Three bottles of equal capacity are containing a mixture of milk and water in ratio 2: 1, 3:7 and 4: 11 respectively. These three bottles are emptied into a large bottle. What is the ratio of milk and water respectively in this large bottle?
A37:53B37:90C37:30D7:30Three bottles of equal capacity are containing a mixture of milk and water in ratio 2: 1, 3:7 and 4: 11 respectively. These three bottles are emptied into a large bottle. What is the ratio of milk and water respectively in this large bottle?
A37:53B37:90C37:30D7:30
Oranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x, what is th
View SolutionOranges are to be transferred from larger boxes into smaller boxes. When a large box is emptied, the oranges from it fill two smaller boxes and still 10 oranges remain outside. If the number of oranges in a small box are taken to be x, what is the number of oranges in the larger box?
View SolutionOne bottle is half-full of milk and another bottle with twice the capacity is one-quarter full of milk. If water is added so that both the bottles are full and the contents of both are then poured into a third bottle that is empty and large enough to hold the contents of both, what fraction of the contents in the third bottle is milk? 14 (b) 13 (c) 23 (d) 38
View Solution3 small pumps and a large pump are filling a tank. Each of the three small pumps works at 2/3rd the rate of the large pump. If all 4 pumps work at the same time, they should fill the tank in what fraction of the time that it would have taken the large pump alone?
View Solution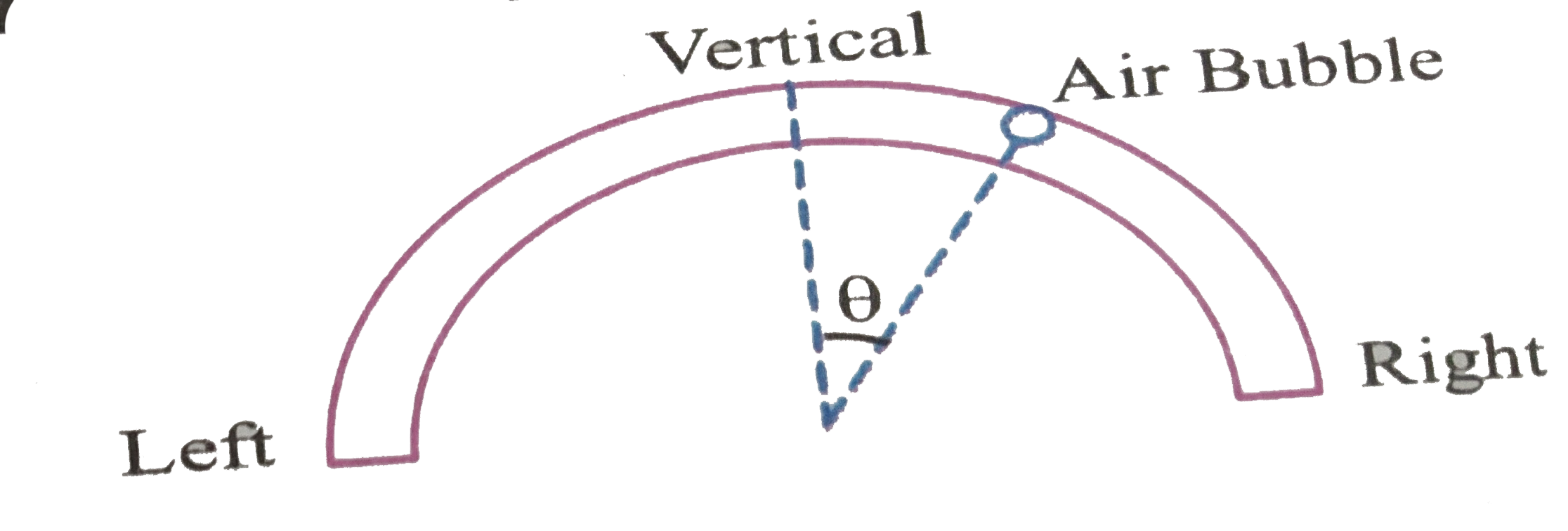
A glass tube filled with colored water, sealed at both the ends is bent into an arc. There is a small air bubble inside. The tube is held with its plane vertical. When the tube moves with constant acceleration either of left or right the bubble shifts and settles at some plane either to the left or right of the highest point. For the situation shown, what can you conclude about acceleration vector of the tube?
View Solution
