If 41a×b23=7 find the values of a and b.
1,5
2,3
3,2
5,1
The correct Answer is:D
To solve the equation 4(1a)×b(23)=7, we will follow these steps:
Step 1: Rewrite the equation
First, we rewrite the fractions in a more manageable form:
4⋅1a⋅b⋅23=7
This can be simplified to:
8b3a=7
Step 2: Cross-multiply
Next, we cross-multiply to eliminate the fraction:
8b=21a
Step 3: Rearranging the equation
We can rearrange this equation to express b in terms of a:
b=21a8
Step 4: Substitute values
Now, we can substitute different values for a to find corresponding values for b. We will check integer values for a to find valid pairs.
Step 5: Testing values
1. Let’s try a=1:
b=21⋅18=218(not an integer)
2. Let’s try a=2:
b=21⋅28=428=214(not an integer)
3. Let’s try a=3:
b=21⋅38=638(not an integer)
4. Let’s try a=4:
b=21⋅48=848=212(not an integer)
5. Let’s try a=5:
b=21⋅58=1058(not an integer)
6. Let’s try a=8:
b=21⋅88=21(integer)
Step 6: Conclusion
The values we found are:
a=8,b=21
First, we rewrite the fractions in a more manageable form:
4⋅1a⋅b⋅23=7
This can be simplified to:
8b3a=7
Next, we cross-multiply to eliminate the fraction:
8b=21a
We can rearrange this equation to express b in terms of a:
b=21a8
Now, we can substitute different values for a to find corresponding values for b. We will check integer values for a to find valid pairs.
1. Let’s try a=1:
b=21⋅18=218(not an integer)
b=21⋅28=428=214(not an integer)
b=21⋅38=638(not an integer)
b=21⋅48=848=212(not an integer)
b=21⋅58=1058(not an integer)
b=21⋅88=21(integer)
The values we found are:
a=8,b=21
Topper's Solved these Questions
- FRACTIONS AND DECIMALSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - FRACTIONS AND DECIMALSEXERCISE - QUESTIONS BANK
30 Videos
- FACTORIZATION OF ALGEBRAIC EXPRESSIONS BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - FACTORIZATION OF ALGEBRAIC EXPRESSIONS EXERCISE - SELF ASSESSMENT SHEET-8
10 Videos
- HCF AND LCMBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - HCF AND LCMEXERCISE - SELF ASSESSMENT SHEET-3
10 Videos
Similar Questions
Knowledge Check
If 123+27×x7=114×23+16 then find the value of x.
A0.006B16C0.6D6If ab=34 then find the value of 7a−4b:3a+b.
A7:1B5:13C12:1DNone of these
If x=53 and x=−12 are the zeroes of the polynomial ax2−7x+b, then find the values of a and b.
View SolutionIf 3a+7b3a−7b=43 then find the value of the ratio 3a2−7b23a2+7b2
View SolutionIf 1+132+1.41.2.134+1.4.71.2.3.136+... then =(a)13, find the value of a.
View SolutionFind the value of ∣∣∣−1724∣∣∣
View Solution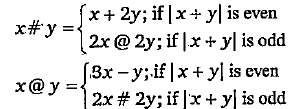
Find the value of 2#((7@(4#5)@3) :
View SolutionIf 15a2+4b215a2−4b2=477 then find the values of the following (i) ab (ii) 7a−3b7a+3b (iii) b2−2a2b2+2a2
View Solution
