The straight lines AB and CD intersect at E . If EF and EG are bisectors of ∠DEAand∠AEC respectively and if ∠AEF=xand∠AEG=y , then
x+y>.90∘
x+y<90∘
x+y=90∘
x+y=180∘
The correct Answer is:C
Step by step video, text & image solution for The straight lines AB and CD intersect at E . If EF and EG are bisectors of angleDEAandangleAEC respectively and if angleAEF=xand angleAEG=y , then by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINES AND ANGLES Book:S CHAND IIT JEE FOUNDATIONChapter:LINES AND ANGLES Exercise:SELF ASSESSMENT SHEET
Explore 10 Videos
- LINES AND ANGLES Book:S CHAND IIT JEE FOUNDATIONChapter:LINES AND ANGLES Exercise:SELF ASSESSMENT SHEET
Explore 10 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBook:S CHAND IIT JEE FOUNDATIONChapter:LINEAR EQUATIONS IN ONE VARIABLEExercise:Unit Test -2
Explore 20 Videos
- NUMBERSBook:S CHAND IIT JEE FOUNDATIONChapter:NUMBERSExercise:SELF ASSESSMENT SHEET-1
Explore 10 Videos
Similar Questions
Knowledge Check
In the given figure, straight lines AB and CD intersect at O.If ∠β = 3∠p,then ∠p is equal to
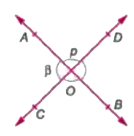 A40∘B45∘C50∘D55∘
A40∘B45∘C50∘D55∘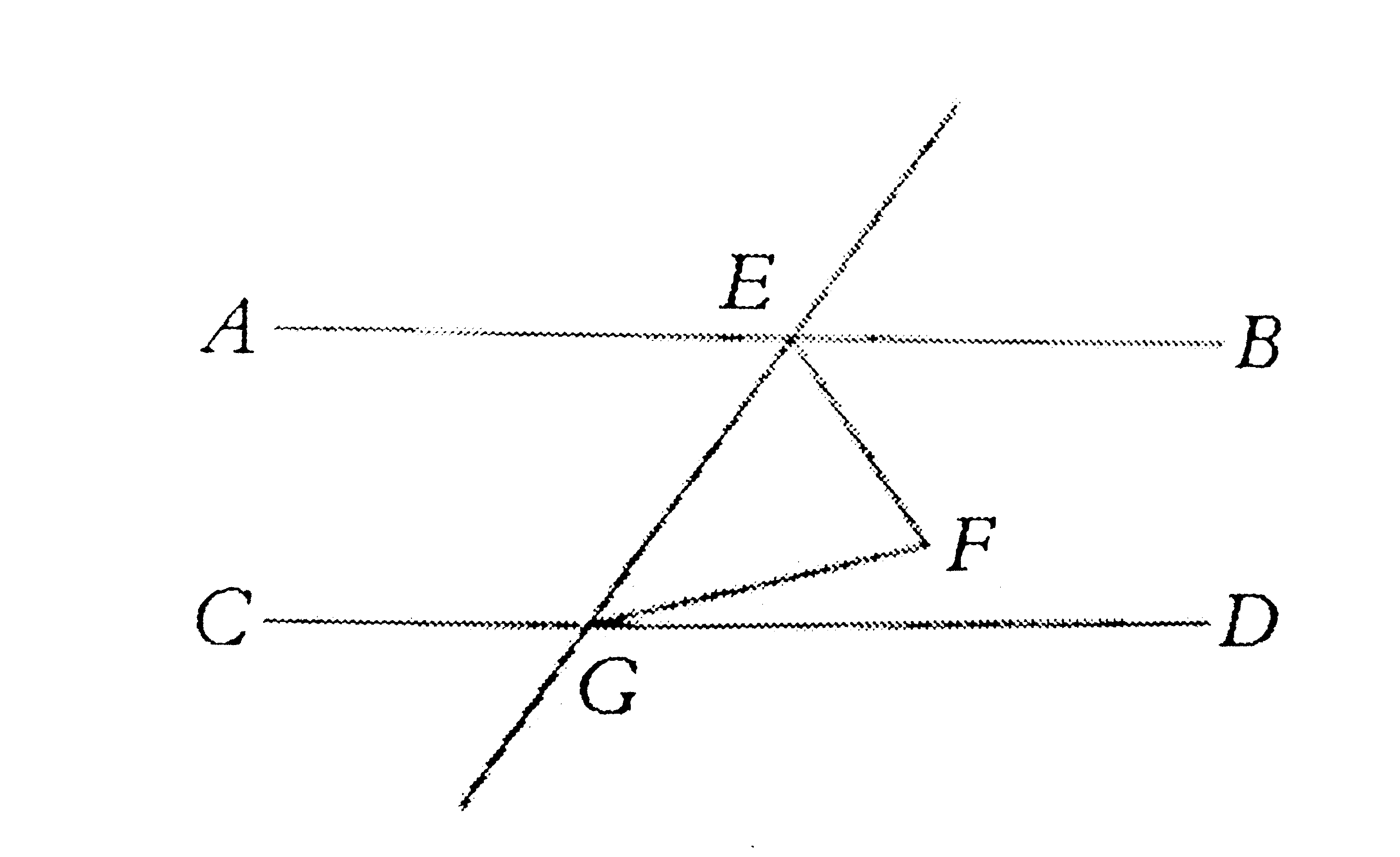
In the figure above, AB || CD. EF and FG are the bisectors of ∠BEGand∠DGE, respectively. ∠FEG=∠FGE+10∘. Find ∠FGE.A20∘B25∘C40∘D35∘In the figure , AB||CD, EG & FG are Bi sectors of ∠BEF & ∠DFE respectively , the m∠FGE is -
 A45∘B90∘C60∘D100∘
A45∘B90∘C60∘D100∘
In the given figure, AB∣∣CD and a transversal t cuts them at E and F respectively. If EG and FG are this bisectors of ∠BEF and ∠EFD respectivelym prove that ∠EGF=90∘.

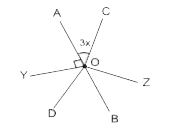
View SolutionAB and CD are intersecting lines. OD is bisector of ∠BOY. Find x.
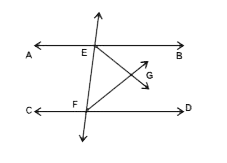
View SolutionIn the given figure, AB∣∣CD and a transversal t cuts them at E and F respectively. If EP and FQ are the bisectors of ∠AEF and ∠EFD respectively, prove that EP∣∣FQ.

View SolutionIn the given figure, straight lines AB and CD intersect at O. If ∠AOC=ϕ, ∠BOC=θ and θ=3ϕ, then ϕ=?
View SolutionThe line segments AB and CD intersect at O. OF is the internal bisector of obtuse angle BOC and OE is the internal bisector of acute angle AOC. If ∠BOC=130∘, what is the measure of ∠FOE?
View Solution
