Two complementary angles are such that two times the measure of one is equal to three times the measure of the other .the measure of the larger angle is :
72∘
108∘
36∘
54∘
The correct Answer is:D
To solve the problem of finding the measure of the larger angle among two complementary angles where two times the measure of one angle is equal to three times the measure of the other, we can follow these steps:
1. Define the angles: Let the two angles be x and y.
2. Set up the complementary angle equation: Since the angles are complementary, we know that:
x+y=90∘(Equation 1)
3. Set up the relationship between the angles: According to the problem, two times the measure of one angle is equal to three times the measure of the other. We can express this as:
2x=3y(Equation 2)
4. Substitute Equation 1 into Equation 2: From Equation 1, we can express y in terms of x:
y=90−x
Now substitute this into Equation 2:
2x=3(90−x)
5. Solve for x: Expand and rearrange the equation:
2x=270−3x
Add 3x to both sides:
2x+3x=270
5x=270
Divide both sides by 5:
x=2705=54∘
6. Find y: Now substitute x back into Equation 1 to find y:
y=90−x=90−54=36∘
7. Identify the larger angle: The two angles are 54∘ and 36∘. Therefore, the measure of the larger angle is:
Larger angle=54∘
Final Answer:
The measure of the larger angle is 54∘.
2. Set up the complementary angle equation: Since the angles are complementary, we know that:
x+y=90∘(Equation 1)
2x=3y(Equation 2)
y=90−x
Now substitute this into Equation 2:
2x=3(90−x)
2x=270−3x
Add 3x to both sides:
2x+3x=270
5x=270
Divide both sides by 5:
x=2705=54∘
y=90−x=90−54=36∘
Larger angle=54∘
The measure of the larger angle is 54∘.
Topper's Solved these Questions
- LINES AND ANGLES Book:S CHAND IIT JEE FOUNDATIONChapter:LINES AND ANGLES Exercise:SELF ASSESSMENT SHEET
Explore 10 Videos
- LINES AND ANGLES Book:S CHAND IIT JEE FOUNDATIONChapter:LINES AND ANGLES Exercise:SELF ASSESSMENT SHEET
Explore 10 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBook:S CHAND IIT JEE FOUNDATIONChapter:LINEAR EQUATIONS IN ONE VARIABLEExercise:Unit Test -2
Explore 20 Videos
- NUMBERSBook:S CHAND IIT JEE FOUNDATIONChapter:NUMBERSExercise:SELF ASSESSMENT SHEET-1
Explore 10 Videos
Similar Questions
Two complementary angles are such that two times the measure of one is equal to three times the measure of the other. The measure of the smaller angle is (a) 45∘ (b) 30∘ (c) 36∘ (d) none of these
View SolutionIf two supplementary angles have equal measure, what is the measure of each angles?
View Solution
Knowledge Check
Two complementary angles are such that twice the measure of the one is equal to three times the measure of the other. The largest of the two measures.
A72∘B54∘C63∘D36∘The measure of an angle is four times the measure of its complementary angle. Then, the measure of that angle is ............
A18∘B72∘C40∘D10∘The measure of an angle for which the measure of the supplement is four times the measure of the complement is
A75∘B30∘C45∘D60∘
The three angles of a triangle are equal to one another. What is the measure of each of the angles?
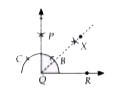
View SolutionMeasure of ∠XQR equals ____.
View SolutionABC is a triangle in which 35 times the smallest angle is equal to the 26 times largest angle. What is the measure of the second largest angle?
View SolutionThe largest bond angle in
View SolutionThe measure of an angle is twice the measure of its supplementary angle. Then, the measure of that angle is .............
View Solution
