Lines and touch a circle C1 of diameter 6. If the center of C1, lies in the first quadrant then the equation of the circle C2, which is concentric with C1, and cuts intercept of length 8 on these lines Solution in Bengali
According to the question, circles are drawn as shown in the figure.
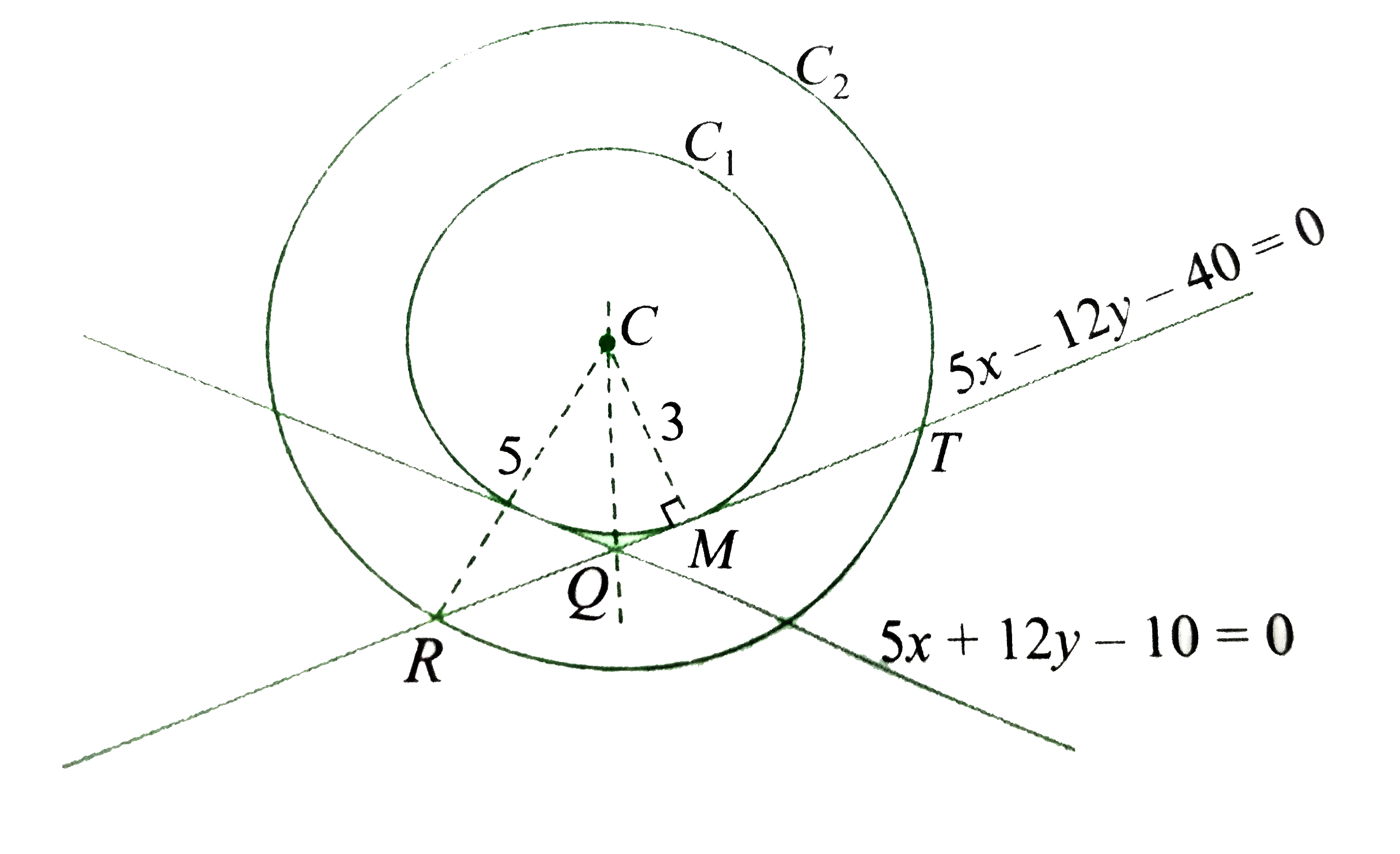
Centre of the circles lies on one of the angle bisectors of the given lines.
or and
But centre lies in first quadrant.
So, for centre , .
Distance of centre (C(5,y) from the line is 3.
(As centre lies in first quadrant)
Sol, centre is (5,2).
Alsok, in right angles triangle CMR, as .
Hence, equation of circle is .
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.2
2 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 4
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the equation of the circle which touches the x-axis and whose center is (1, 2).
View SolutionPARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionThe centres of two circles C1 and C2 each of unit radius are at a distance of 6 units from each other. Let P be the mid point of the line segment joining the centres of C1 and C2 and C be a circle touching circles C1 and C2 externally. If a common tangent to C1 and C passing through P is also a common tangent to C2 and C, then the radius of the circle C is
View SolutionC1 and C2 are two concentric circles, the radius of C2 being twice that of C1. From a point P on C2, tangents PA and PB are drawn to C1. Then the centroid of the triangle PAB (a) lies on C1 (b) lies outside C1 (c) lies inside C1 (d) may lie inside or outside C1 but never on C1
View SolutionEquation of circle whose centre (4,3) and touching line 5x+12y-10=0
View Solutionउस वृत्त का समीकरण ज्ञात कीजिए केंद्र (3,-4) है तथा रेखा 5x+12y−12=0 को छूता है ।
View Solutionउस वृत्त का समीकरण निकालें जो रेखा 5x+12y=1 को स्पर्श करता है और जिसका केंद्र (3,4) है।
View SolutionLines 5x+12y−10=0 and 5x−12y−40=0touch a circle C1 of diameter 6.If the centre of C1 lies in the first quadrant, find the equation of the circle C2 which is concentric with C1 and cuts, intercepts of length 8 on these lines.
View SolutionA circle C1 of diameter 6 units, is in the first quadrant and it touches the striaght lines 5x+12y−10=0and5x−12y−40=0. Another circle C2 concentric with C1 intercepts chords of length 8 units. Form the two given straight lines. Find the equation of the cirlce C2.
View Solutionरेखाएँ 5x+12y−10=0 और 5x−12y−40=0 एक वृत्त C1 को स्पर्शी करती है जिसका व्यास 6 इकाई है। यदि C1 का केंद्र प्रथम चतुथार्श में हो तो वृत्त C2 का समीकरण ज्ञात कीजिए जो C1 के संकेन्द्रिय है और रेखाओं से 8 इकाई लम्बाई का अन्तः खंड काटता है।
View Solutionउस वृत्त का समीकरण ज्ञात कीजिए, जो सरल रेखा 5x+12y−1=0 को स्पर्श करें एवं केन्द्र (3, 4) हों।
View SolutionThe equation of the circle withcentre at (4,3) and touching the line 5x−12y−10=0 is
View SolutionLines 5x+12y−10=0 and 5x−12y−40=0 touch a circle C1 of diameter 6. If the center of C1, lies in the first quadrant then the equation of the circle C2, which is concentric with C1, and cuts intercept of length 8 on these lines
View Solution
