Tangents are drawn to the circle x2+y2=a2 from two points on the axis of x, equidistant from the point (k,0). Show that the locus of their intersection is ky2=a2(k−x).Solution in Bengali
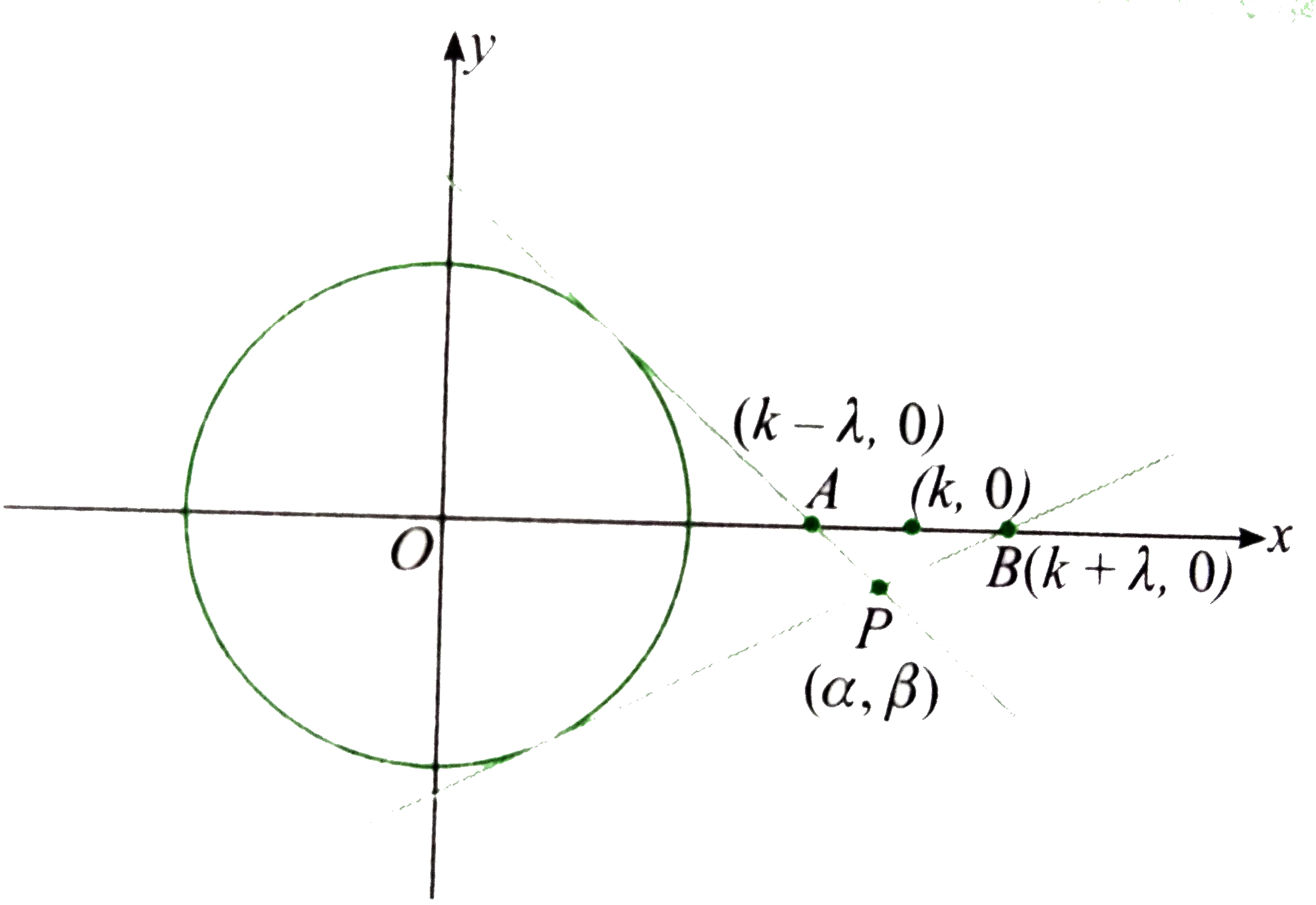
As shown in figure , point A and B are equidistant from point (k,0).
Tangents drawn from point A and B intersect at point P(α,β).
Equation of pair of tangents from point P is
(x2+y2−a2)(α2+β2−a2)=(αx+βy−a2)2 (Using T2=SS1)
This equation is satisfied by points A and B .
∴((k−λ)2−a2)(α2+β2−a2)=(α(k−λ)−a2)2 (1)
and ((k+λ)2−a2)(α2+β2−a2)=(α(k+λ)−a2)2 (2)
Subtracting (1) and (2) , we get
(α2+β2−a2)(4kλ)=[(k+λ)α−a2+(k−λ)α−a2][(k+λ)α−(k−λ)α]=[2(kα−a2)][2λα]=4λα[kα−a2]
⇒k(α2+β2−a2)=kα2−a2α
⇒kβ2=a2(k−α)
Hence, the locu is ky2=a2(k−x)
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.2
2 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - For problems 3 and 4
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the equation of the circle which touches the x-axis and whose center is (1, 2).
View SolutionPARAGRAPH X Let S be the circle in the xy -plane defined by the equation x2+y2=4. (For Ques. No 15 and 16) Let E1E2 and F1F2 be the chords of S passing through the point P0(1, 1) and parallel to the x-axis and the y-axis, respectively. Let G1G2 be the chord of S passing through P0 and having slope −1 . Let the tangents to S at E1 and E2 meet at E3 , the tangents to S at F1 and F2 meet at F3 , and the tangents to S at G1 and G2 meet at G3 . Then, the points E3, F3 and G3 lie on the curve x+y=4 (b) (x−4)2+(y−4)2=16 (c) (x−4)(y−4)=4 (d) xy=4
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionThe locus of the point of intersection of the two tangents drawn to the circle x^(2)+y^(2)=a^(2) which include are angle alpha is
View SolutionTangents are drawn to the circle x2+y2=a2 from two points on the axis of x, equidistant from the point (k,0). Show that the locus of their intersection is ky2=a2(k−x).
View SolutionA tangent is drawn to each of the circles x2+y2=a2 and x2+y2=b2. Show that if the two tangents are mutually perpendicular, the locus of their point of intersection is a circle concentric with the given circles.
View SolutionIf chord of contact of the tangent drawn from the point (a,b) to the ellipse (x^(2))/(a^(2))+(y^(2))/(b^(2))=1 touches the circle x^(2)+y^(2)=k^(2), then find the locus of the point (a,b).
View SolutionThe locus of the point of intersection of the tangents to y2=4x+yandy2=8x+16 which are perpendicular to each other is x=−k. Then k=
View SolutionNumber of integral value(s) of k for which no tangent can be drawn from the point (k,k+2) to the circle x2+y2=4 is :
View SolutionThe locus of the feet of the perpendicular drawn from the point (a,0) on tangent to the circle x2+y2=a2 is
View SolutionThe length of the tangent from the point (-1,1) to the circle x2+y2−4x+k=0 equal to 2 then k=
View SolutionThe value of k for which two tangents can be drawn from (k,k) to the circle x^2+y^2+2x+2 y-16=0
View Solutionएक नियत बिंदु (h,k) से वृत्त x2+y2=r2 पर एक छेदक रेखा (secant) खींची जाती है। दिखाइए की वृत्त पर खींची गई छेदक रेखाओं के मध्य-बिंदु का बिन्दुपथ x2+y2=hx+ky है।
View SolutionTangents are drawn to the circle x2+y2=a2 from two points on the axis of x, equidistant from the point (k,0). Show that the locus of their intersection is ky2=a2(k−x).
View Solution
