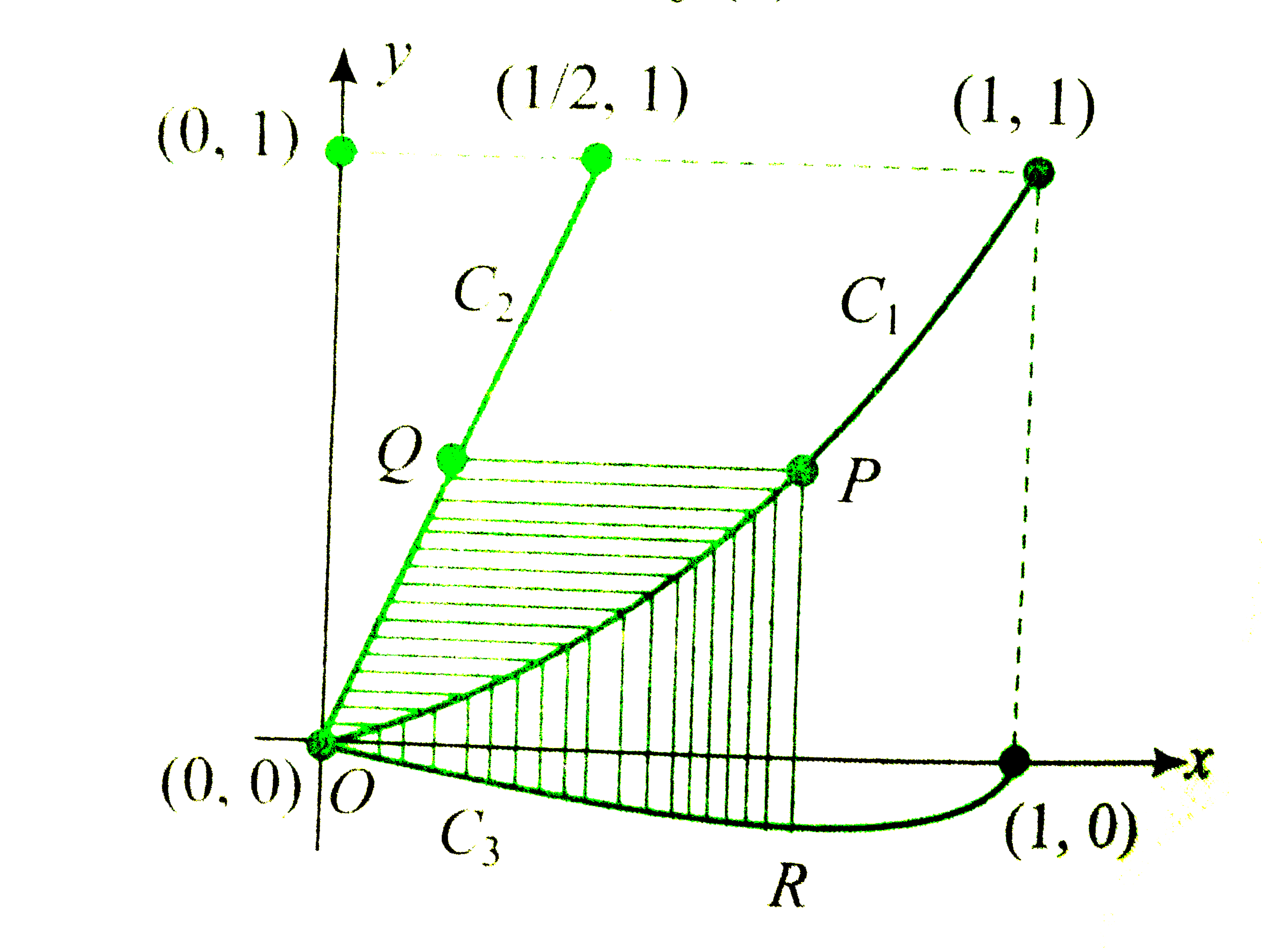
Let C1C2 be the graphs of the functions y=x2 and y=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axis, meet C2 and C3 at Q and R, respectively (see Figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x)Solution in Bengali
Let P be on C1,y=x2be(t,t2)
∴ y co-ordinate of Q is also t2
Now, Q on y =2x where y=t2
∴ x=t2/2
∴ Q(t22,t2)
For point R, x=t and it is on y=f(x)
∴ R(t,f(t))
Given that,
Area OPQ = Area OPR
⇒ ∫t20(√y−y2)dy=∫t0(x2−f(x))dx
Differentiating both sides w.r.t. t, we get
(√t2−t22)(2t)=t2−f(t)
⇒ f(t)=t3−t2
⇒ f(x)=x3−x2
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
Find the area bounded by the curve x2=y,x2=−yandy2=4x−3
View SolutionFind the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionLet f(x)=M a xi mu m{x2,(1−x)2,2x(1−x)}, where 0≤x≤1. Determine the area of the region bounded by the curves y=f(x),x-axis ,x=0,andx=1.
View SolutionLet C_1 and C_2, be the graph of the functions y= x^2 and y= 2x, 0<=x<= 1 respectively. Let C_3, be the graph of a function y- (fx), 0<=x<=1, f(0)=0. For a point Pand C_2, let the lines through P, parallel to the axes, meet C_2 and C_3, at Q and R respectively. If for every position of P (on C_1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View SolutionThe points of discontinuity of the function f(x)={2√x , 0≤x≤1, 4−2x , 1<x
View SolutionLet C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View SolutionLet f be a function such that f(x+f(y))=f(f(x))+f(y) ∀x,y∈R and f(h)=h for 0ε
where ε>0, then determine f'(x) and f(x).
View Solutionमाना C1 और C2 क्रमशः फलन y=x2 औरy=2x,0≤x≤1 के ग्राफ हैं। माना C3 फलन, y=f(x),0≤x≤1,f(0)=0 का ग्राफ है। C1 के एक बिंदु P के लिए माना कि बिन्दु P से होकर जाने वाली तथा अक्षों के समान्तर रेखायें C2 व C3 को क्रमशः Q और R पर मिलती है।
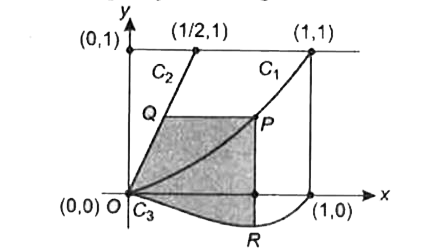 यदिP की प्रत्येक स्थिति ( C1 पर ) के लिए छायांकित क्षेत्र OPQ और ORP का क्षेत्रफल समान हो,तो फलन f(x) को ज्ञात कीजिए।
यदिP की प्रत्येक स्थिति ( C1 पर ) के लिए छायांकित क्षेत्र OPQ और ORP का क्षेत्रफल समान हो,तो फलन f(x) को ज्ञात कीजिए।
View SolutionLet f:[0,1]→[0,1] be a continuous function. Then prove that f(x)=x for at least one 0≤x≤1.
View SolutionIn the hexaploid wheat, the haploid (n) and basic (x) numbers of chromosomes are
View SolutionLet C1C2 be the graphs of the functions y=x2 and y=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axis, meet C2 and C3 at Q and R, respectively (see Figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x)
View SolutionLet C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).

View SolutionThe points of discontinuity of the function f(x)={2√x , 0≤x≤1, 4−2x , 1<x
View SolutionLet f:[0,1]→[0,1] be a continuous function. Then prove that f(x)=x for at least one 0≤x≤1.
View Solution
