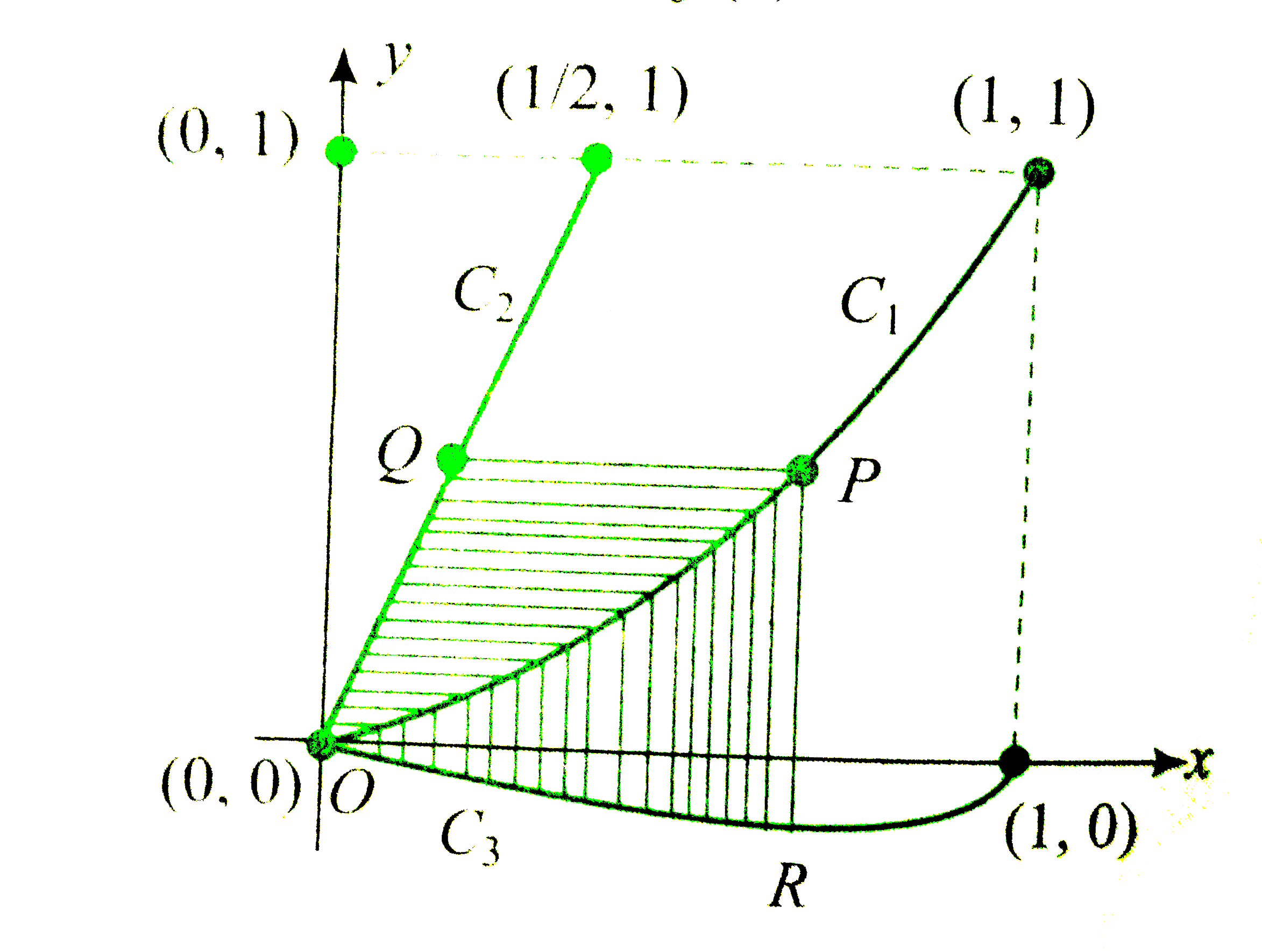
Let C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
 Solution in Tamil
Solution in Tamil
Let P be on C1,y=x2be(t,t2)
∴ y co-ordinate of Q is also t2
Now, Q on y =2x where y=t2
∴ x=t2/2
∴ Q(t22,t2)
For point R, x=t and it is on y=f(x)
∴ R(t,f(t))
Given that,
Area OPQ = Area OPR
⇒ ∫t20(√y−y2)dy=∫t0(x2−f(x))dx
Differentiating both sides w.r.t. t, we get
(√t2−t22)(2t)=t2−f(t)
⇒ f(t)=t3−t2
⇒ f(x)=x3−x2
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.19videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise 9.214videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Find the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionFind the area lying in the first quadrant and bounded by the curve y=x3 and the line y=4x.
04:21View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
07:49View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
10:33View SolutionLet C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
 View Solution
View SolutionConsider circles
C1:x2+y2+2x−2y+p=0
C2:x2+y2−2x+2y−p=0
C3:x2+y2=p2
Statement-I: If the circle C3 intersects C1 orthogonally then C2 does not represent a circle
Statement-II: If the circle C3 intersects C2 orthogonally then C2 and C3 have equal radii Then which of the following is true?View SolutionEvaluate ∣∣ ∣∣.xC1.xC2.xC3.yC1.yC2.yC3.xC1.zC2.zC3∣∣ ∣∣
View SolutionLet C1 and C2 denote the centres of the circles x2+y2=4 and (x−2)2+y2=1 respectively and let P and Q be their points of intersection. Then the areas of triangles C1PQ and C2PQ are in the ratio _
View SolutionLet n be a positive integer and
(1+x)n+C0+C1x+C2x2+C3x3+...+Crxr+...+Cn−1xn−1+Cnxn
Where Cr stands for .nCr, then
Q. The value of ∑∑0≤r<s≤n(Cr±CS)2 isView SolutionIf f(x) is a differentiable function wherever it is continuous and f'(c1)=f'(c2)=0,f''(c1).f''(c2)<0,f(c1)=5,f(c2)=0and(c1<c2)
If f(x) is continuous in [c1,c2]andf''(c1)−f''(c2)>0, then minimum number of roots of f'(x)=0 in [c1−1,c2+1] isView SolutionIf f(x) is a differentiable function wherever it is continuous and f'(c1)=f'(c2)=0,f''(c1).f''(c2)<0,f(c1)=5,f(c2)=0and(c1<c2)
If f(x) is continuous in [c1,c2]andf''(c1)−f''(c2)<0, then minimum number of roots of f'(x)=0 in c1−1,c2+1] is05:45View SolutionIf f(x) is a differentiable function wherever it is continuous and f'(c1)=f'(c2)=0,f''(c1).f''(c2)<0,f(c1)=5,f(c2)=0and(c1<c2)
If f(x) is continuous in [c1,c2] and f''(c1)−f''(c2)>0, then minimum number of roots of f(x)=0 in [c2−1,c2+1] is04:31View Solutionमाना C1 और C2 क्रमशः फलन y=x2 औरy=2x,0≤x≤1 के ग्राफ हैं। माना C3 फलन, y=f(x),0≤x≤1,f(0)=0 का ग्राफ है। C1 के एक बिंदु P के लिए माना कि बिन्दु P से होकर जाने वाली तथा अक्षों के समान्तर रेखायें C2 व C3 को क्रमशः Q और R पर मिलती है।
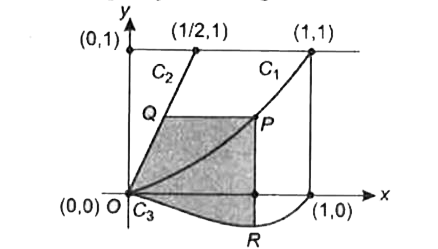 यदिP की प्रत्येक स्थिति ( C1 पर ) के लिए छायांकित क्षेत्र OPQ और ORP का क्षेत्रफल समान हो,तो फलन f(x) को ज्ञात कीजिए। 07:14View Solution
यदिP की प्रत्येक स्थिति ( C1 पर ) के लिए छायांकित क्षेत्र OPQ और ORP का क्षेत्रफल समान हो,तो फलन f(x) को ज्ञात कीजिए। 07:14View Solutionयदि (1+x)n=C0+C1x+C2x2+....+Cnxn तब C0−(C0+C1)+(C0+C1+C2)−(C0+C1+C2+C3) जहाँ n रागपूर्णांक है
05:51View SolutionLet C1C2 be the graphs of the functions y=x2 and y=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axis, meet C2 and C3 at Q and R, respectively (see Figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x)
06:23View Solution

