Consider an acute angled ΔABC. Let AD, BE and CF be the altitudes drawn from the vertice to the opposite sides. Prove that : EFa+FDb+DEc=R+rR. Solution in Bengali
FEa+FDb+DEc=acosAa+bcosBb+ccosCa
=cosA+cosB+cosC
≤32
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.10
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.11
4 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.8
7 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE )
8 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - All Questions
1119 Videos
Similar Questions
In ΔABC, if r1<r2<r3, then find the order of lengths of the sides
View SolutionRegular pentagons are inscribed in two circles of radius 5and 2 units respectively. The ratio of their areas is
View SolutionIf the incircle of the triangle ABC passes through its circumcenter, then find the value of 4sin.A2sin.B2sin.C2
View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1|(k^2-3k+1)S_k| is ____________
View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then find f−1(x)
View SolutionIn an acute angle triangle ABC,AD,BE and CF are the altitudes,then (EF)/(a)+(FD)/(b)+(DE)/(c) is equal to -
View SolutionIn an acute angled triangle ABC, let AD,BE and CF be the perpendicular opposite sides of the triangle. The ratio of the product of the side lengths of the triangles DEF and ABC, is equal to
View SolutionIf in a ΔABC,AD,BEandCF are the altitudes and R is the circumradius, then find the radius of the DEF.
View SolutionIn an acute angle ΔABC, let AD, BE and CF be the perpendicular from A, B and C upon the opposite sides of the triangle. (All symbols used have usual meaning in a tiangle.)
The orthocentre of the ΔABC, is the
View SolutionIn a scalene triangle ABC , AD and CF are the altitudes drawn from A and C on the sides BC and AB respectively. If the area of the triangle ABC and BDF are 18sq.units and 2 sq. units respectively and DF = 2√2 , then R =
View SolutionΔABC లో AD, BE , CF లు A,B C శీర్షాల నుంచి ఎదుటి భుజాలకు గీసిన లంబాలయితే 1 / AD + 1 / BE + 1 CF = 1 /r అని చూపండి.
View SolutionThe altitudes from the vertices A,B,C of an acute angled triangle ABC to the opposite sides meet the circumcircle at D,E,F respectively . Then EFBC=
View SolutionIn ΔABC and ΔDEF , AB = DE, AB∣∣DE, BC = EF and BC∣∣EF. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
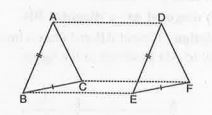 Show that AD∣∣CF and AD=CF.
Show that AD∣∣CF and AD=CF.
View SolutionIn ΔABC, if AD , BE , CF are the perpendiculars drawn from the vertices A, B, C to the opposite sides, shot that
1AD+1BE+1CF=1rand(ii)AD.BE.CF=(abc)28R3=8Δ3abc
View SolutionIn an acute angled triangle ABC, let AD,BE and CF be the perpendicular opposite sides of the triangle. The ratio of the product of the side lengths of the triangles DEF and ABC, is equal to
View SolutionIn an acute angle ΔABC, let AD, BE and CF be the perpendicular from A, B and C upon the opposite sides of the triangle. (All symbols used have usual meaning in a tiangle.)
The orthocentre of the ΔABC, is the
View Solution
