An arc AC of a circle subtends a right angle at then the center O. the point B divides the arc in the ratio 1:2, If →OA=a&→OB=b. then the vector →OC in terms of a&b, isSolution in Bengali
1. vector →c is coplanar with vector →aand→b. Therefore,
→c=x→a+y→b
Point B didvides arc AC in the ratio 1:2 so that ∠AOB=30∘and∠BOC=60∘
we have to find the values of x and y when we arew given
|→a|=∣∣→b∣∣=|→c|=r(say).
→a.→b=r2cos30∘=r2√32and→a.→b=0
→b.→c=r2cos60∘=r22
Multiplying both sides of (i) scalarly by →cand→a,→c.→c=x→a.→c+y→b.→c
and →c.→a=x→a.→a+y→b.→a
r2=0+r22y,y=2
and0=xr2+yr2√32
putting y=2,x=−√3
→c=−√3→a+2→b
→c=−√3→a+2→b

Related Playlists
- BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.118videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.215videos
DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - All Questions262videos
DETERMINANTS
- BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - All Questions578videos
DIFFERENTIAL EQUATIONS
Similar Questions
Find |→a|and∣∣→b∣∣,if(→a+→b).(→a−→b)=8and|→a|=8∣∣→b∣∣
03:34View SolutionIf →a=2ˆi+3ˆj−5ˆk,→b=mˆi+nˆj+12ˆkand→a×→b=→0, then find (m,n).
03:27View SolutionIf P = {1,2}, form set set P×P×P
02:24View SolutionFor each of the following differential equations verify that the accompanying functions a solution. Differential Function
(a)xdydx=y, y=ax
(b)x+ydydx=0, y=±√a2−x2
(c)xdydxy=y2, y=ax+a
(d)x3d2ydx2=1, y=ax+b+12x
(e)y=(dydx)2, y=14(x±a)205:15View SolutionIn two congruent circles with centres O and O', if arc AXB subtends an angle of 75^(@) at the centre O and arcA'YB' subtends an angle of 25^(@) at the center O, Then find the ratio of arcs AXB and A'YB'
07:44View SolutionAn arc AC of a circle subtends a right angle at then the center O. the point B divides the are in the ratio 1:2, If vec OA=a&vec OB=b .then the vector vec OC in terms of a&b, is
01:05View SolutionShow that any angle in a semi-circle is a right angle.
The following arc the steps involved in showing the above result. Arrange them in sequential order.
A) ∴∠ACB=180∘2=90∘
B) The angle subtended by an arc at the center is double of the angle subtended by the same arc at any point on the remaining part of the circle.
c) Let AB be a diameter of a circle with center D and C be any point on the circle. Join AC and BC.
D) ∴∠AD=2×∠ACB
180∘=2∠ACB(∴∠ADB=180∘)
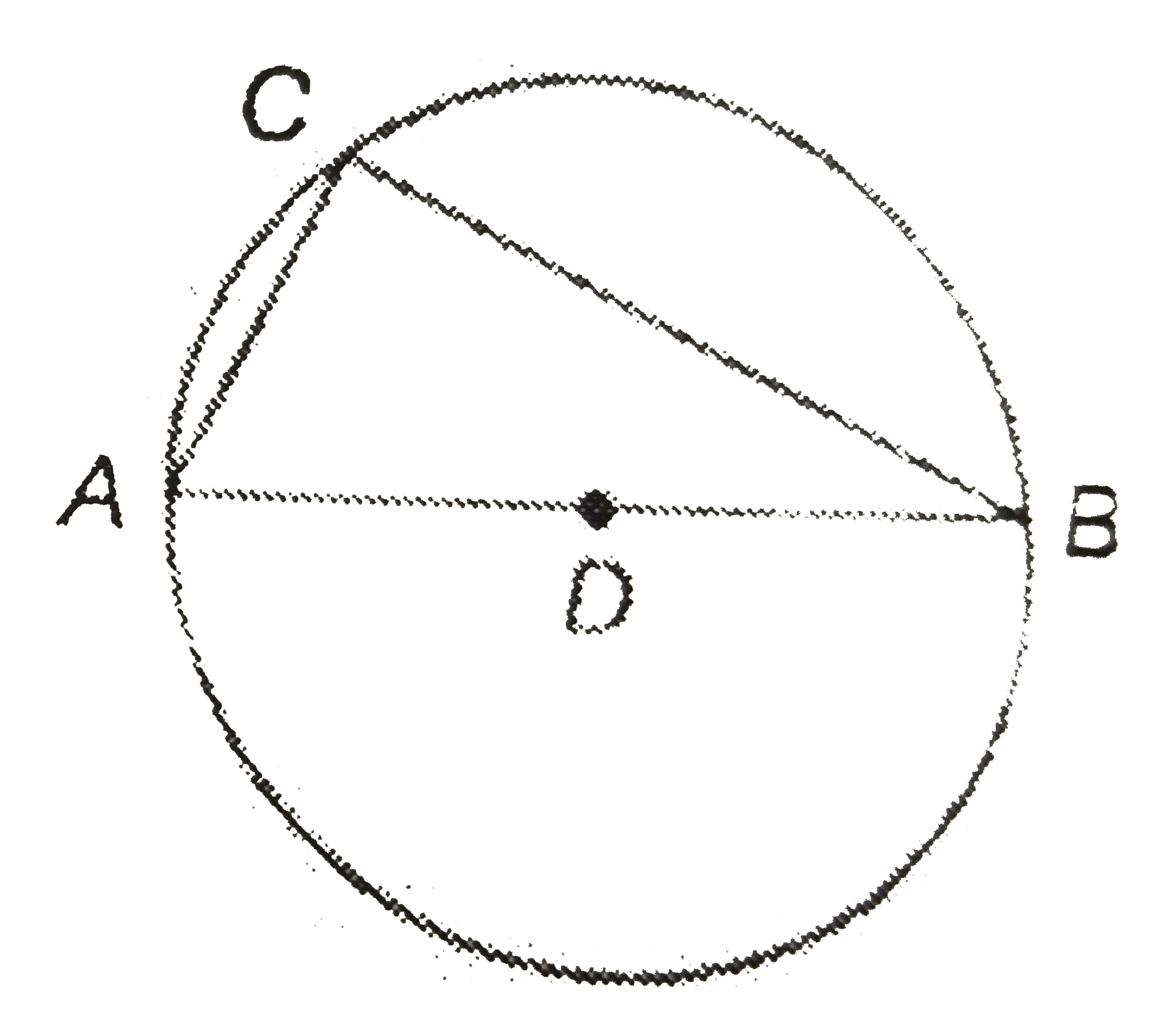 04:56View Solution
04:56View Solutionसिद्ध कीजिए कि किसी चाप द्वारा वृत्त के केंद्र पर बना कोण, इसी चाप द्वारा वृत्त की परिधि के किसी बिंदु पर बने कोण का दुगुना होता है।
01:37View SolutionThe arc AC of a circle subtends a righe angle at the centre O B divides the arc in the ratio 5:1. If ¯¯¯OA=¯aand¯¯¯OB=¯b then show that ¯¯¯¯¯¯OC=2√2b−(√3−1)¯a√3+1
06:56View Solutionबराबर वृत्तों में बराबर चापों द्वारा केन्द्रों पर अन्तरित कोण होते हैं-
05:31View Solutionचित्र में चाप AB द्वारा वृत्त के केन्द्र O पर अन्तरित कोण 120∘ है तथा AC वृत्त का व्यास है, तो ∠OBC का मान लिखिए।
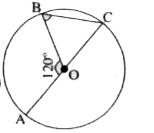 47:48View Solution
47:48View Solutionकिसी चाप द्वारा वृत्त के केन्द्र पर बनाया गया कोण 70∘ है। उसी चाप द्वारा वृत्त के शेष भाग पर स्थित किसी बिन्दु पर बनाया गया कोण होगा
02:18View SolutionAn arc AC of a circle subtends a right angle at then the center O. the point B divides the arc in the ratio 1:2, If →OA=a&→OB=b. then the vector →OC in terms of a&b, is
03:58View SolutionAC एक वृत्त का चाप है जो केंद्र O पर समकोण अंतरित करता है । बिंदु B उस चाप को 1:2 में विभाजित करता है । यदि −−→OA=→a तथा −−→OB=→b है तो →a तथा →b पदों में सदिश −−→OC है
01:28View SolutionAngle subtend by an arc at center is double the angle subtend b it at any point on remaining part OF circle||Angle is a semi circle is a 90 ||Example ||Congurent arc|| Equal arc||Cyclic quadrilateral
02:24View Solution

