If lines 2x−3y+6=0 and kx+2y+2=0 cut the coordinate axes in concyclic points, then the value of |k| is Solution in Bengali
The correct Answer is:3
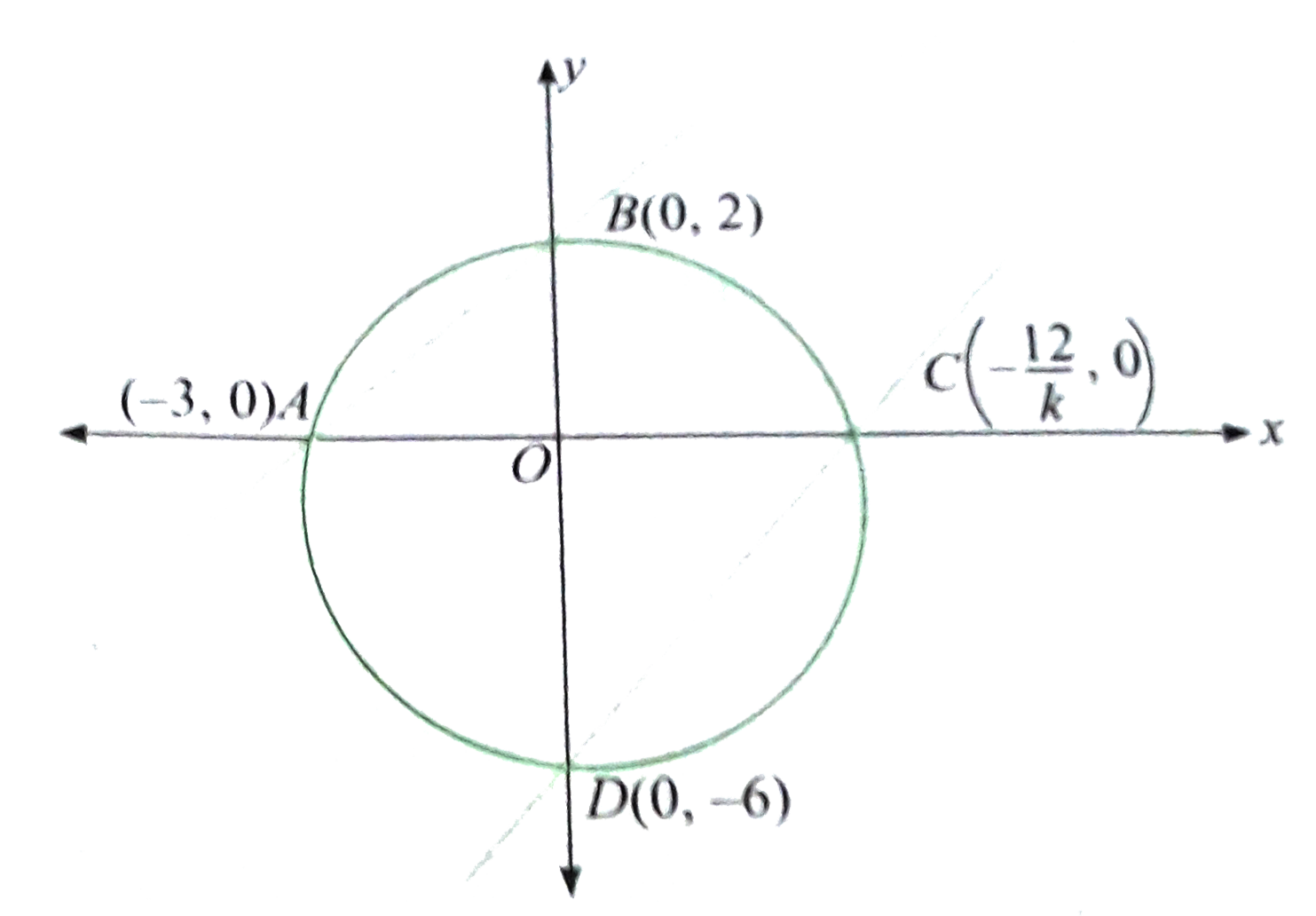
2x−3y+6=0 meets the axes at A(−3,0) and B(0,2). kx+2y+12=0 meets the axes at D(0,−6) and C(−12/k,0), Points A,B.C and D will be concyclic, if
OA×OC=OB×OD
⇒3×(−12/k)=2×6
⇒k=−3
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Matrix match type
4 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
The lines p(p2+1)x−y+q=0 and (p2+1)2x+(p2+1)y+2q=0 are perpendicular to a common line for
View SolutionConsider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:

View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionThe lines 2x+3y+19=0 and 9x+6y−17=0 , cut the coordinate axes at concyclic points.
View SolutionIf the lines x−2y+3=0,3x+ky+7=0 cut the coordinate axes in concyclic points, then k=
View SolutionIf the lines 2x+3y-1=0 and kx-y+4=0 intersect the coordinate axes in concyclic points then k-1=
View SolutionIf lines 2x−3y+6=0 and kx+2y=12=0 cut the coordinate axes in concyclic points, then the value of |k| is
View SolutionIf 2x+3y−6=0 and 9x+6y−18=0 cuts the axes in concyclic points, then the centre of the circle, is
View SolutionIf the lines 2x−3y+7=0,3x+ky+5=0 cut the coordinate axes in concyclie points then k=
View Solutionरेखाएँ 2x+3y+19=0 और 9x+6y−17=0 निर्देशांक अक्षों को चक्रीय बिन्दुओं पर काटती हैं।
View SolutionThe lines ax + 3y + 19 = 0 and 9x + 6y-17 = 0 cut the coordinate axes in concyclic points then a =
View SolutionIf the lines x−2y+3=0,3x+ky+7=0 cut the coordinate axes in concylic points, then k=
View SolutionThe lines 2x+3y+19=0 and 9x+6y−17=0 , cut the coordinate axes at concyclic points.
View SolutionIf lines 2x−3y+6=0 and kx+2y=12=0 cut the coordinate axes in concyclic points, then the value of |k| is
View SolutionThe values of k for which lines kx+2y+2=0,2x+ky+3=0,3x+3y+k=0 are concurrent are
View Solution
