Draw the graph of y=3x−x31−3x2 and hence the graph of y=tan−1.3x−x31−3x2.Solution in Bengali

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We have y=f(x)=tan−1(3x−x31−3x2)
Domain of f(x) is R={−1√3,1√3}
Let x =tanθ,θ∈(−π/2,π/2)
⇒ θ=tan−1x
Now tan−1(3x−x31−3x2)=tan−1(3tanθ−tan3θ1−3tan2θ)
=tan−1(tan3θ)
tan−1(tanα),where α∈(−3π/2,3π/2)
Now consider the graph of y=tan−1(tanα), where α∈(−3π/2,3π/2).
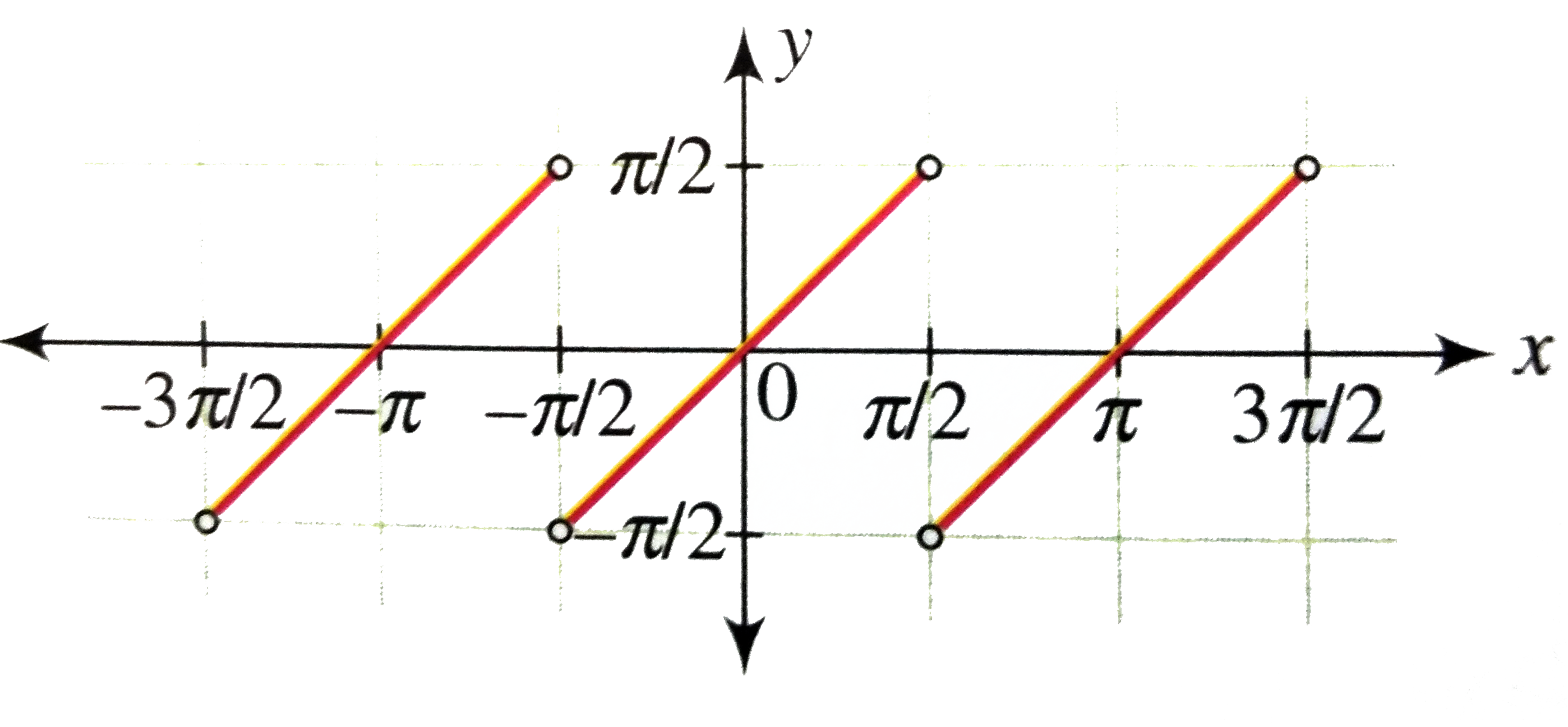
ocr_image
From the graph,
tan−1(3x−x31−3x2)=tan−1(tanα)
=⎧⎪⎨⎪⎩α+π−3π/2<α−π/2α−π/2<α<π/2α−ππ/2<α<3π/2
=⎧⎪ ⎪⎨⎪ ⎪⎩3tan−1x+π−3π/2<tan−1x<−π/23tan−1x−π/2<3tan−1x<π/23tan−1x−ππ/2<3tan−1x<3π/2
=⎧⎪ ⎪⎨⎪ ⎪⎩3tan−1x+π−π/2<tan−1x<−π/63tan−1x−π/6<tan−1x<π/63tan−1x−ππ/6<tan−1x<π/2
=⎧⎪ ⎪⎨⎪ ⎪⎩3tan−1x+π−∞<x<−1/23tan−1x−1/√3<x<1/√33tan−1x−π1/√3<x<∞
tan−1 is an invreasing function for x∈R.
So all brance functions in (i) are increasing functions
limx→−∞(3tan−1x+π)=−π2,limx→−1√3(3tan−1x+π)=π2
3tan−1x+π=0∴x=−√3
Thus, tan−1(3x−x31−3x2) increases from −π2toπ2when x increases from −∞toπ2intersecting the x-axis at x =−√3
limx→∞(3tan−1x−π)=π2,limx→1√3(3tan−1x−π)=−π2
3tan−1x−π=0∴x=−√3
Thus tan−1(3x−x21−3x2) increases form −π2toπ2 when x increases form 1√3 to ∞intersecting the x-axis at x=√3
From this information, we can draw the graph of y=tan−1(3x−x21−3x2) can be drawn as follows.
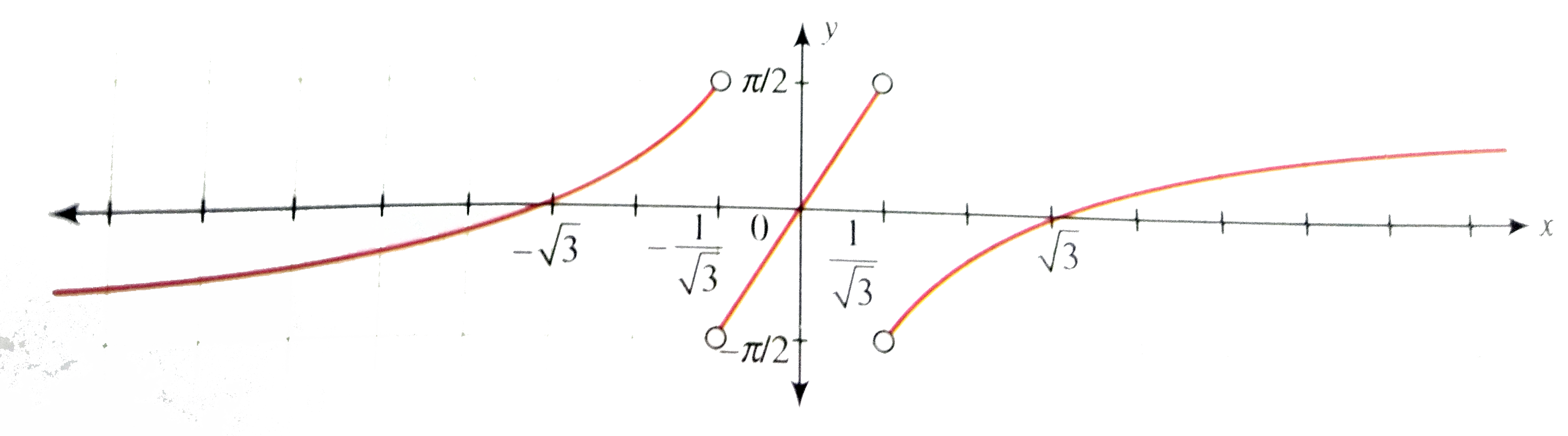
ocr_image

Updated on:21/07/2023
|
Class 12MATHSINVERSE TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions