Find the length of the subtangent to the curve x2y2=a4 at (−a,a).Solution in Bengali
The correct Answer is:3
Area of ΔOAB=12(1)(8) = 4 sq. units
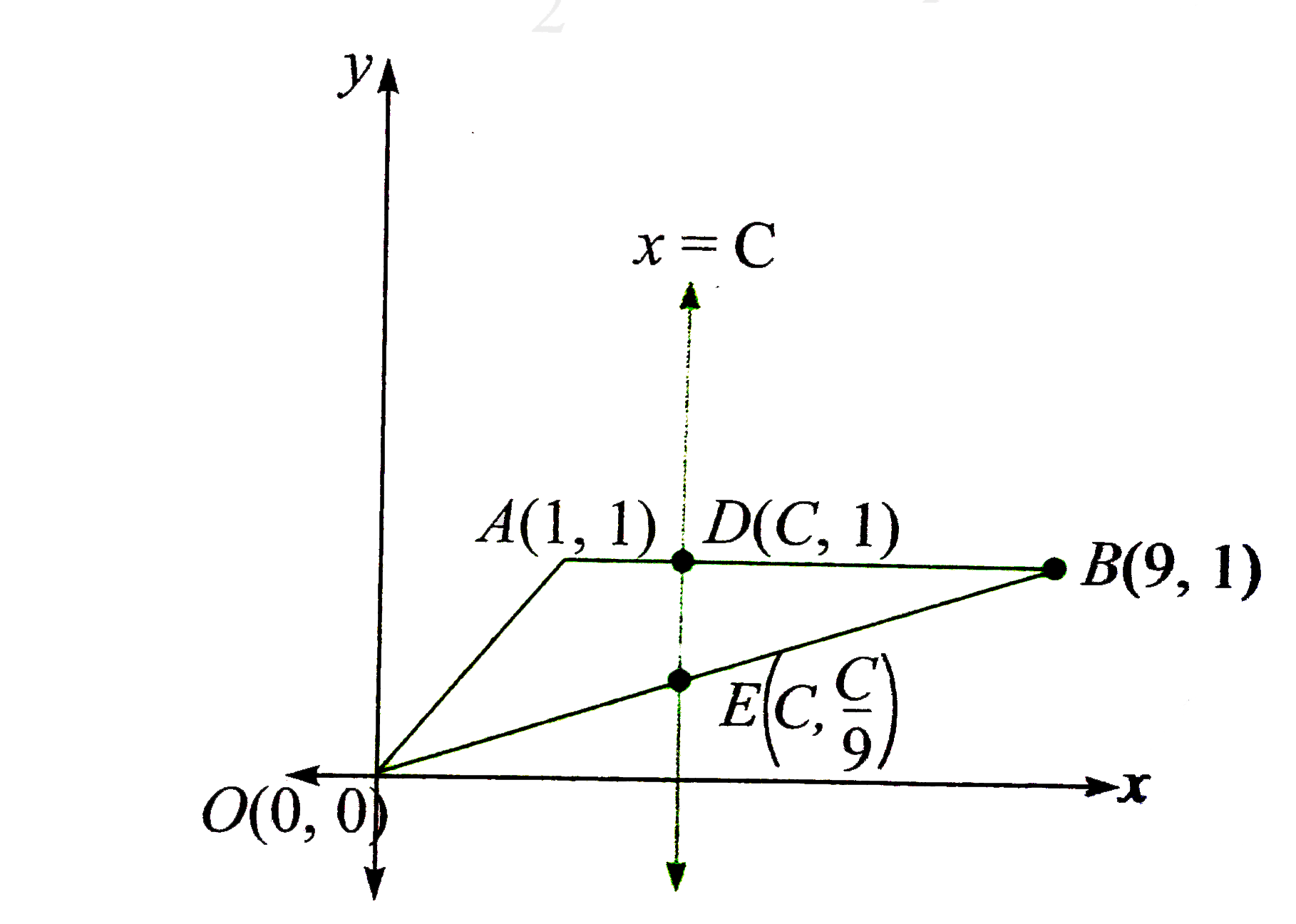
The equation of OB is
y=19x
Hence, the point E is (C, C/9).
Now, the area of ΔBDE is 2 sq. units. Therefore,
or 12(1−C9)(9−C)=2
or (9−C)2=36
or 9−C=±6
or C=3
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (JEE MAIN)9videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (JEE ADVANCED)3videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MATRIX MATCH TYPE)8videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
The line L given by x5+yb=1 passes through the point (13,32).the line K is parallel to L and has the equation xc+y3=1 then the distance between L and K is
03:57View SolutionThe locus of the orthocentre of the triangle formed by the lines (1+p)x−py+p(1+p)=0,(1+q)x−qy+q(1+q)=0 and y = 0, where p≠⋅q, is (A) a hyperbola (B) a parabola (C) an ellipse (D) a straight line
02:09View SolutionMatch the following lists:
 02:08View Solution
02:08View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
01:29View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
04:27View SolutionThe length of subtangent to the curve y=exa
04:13View SolutionThe length of the subtangent at (2,2) to the curve x5=2y4 is
03:10View SolutionThe length of the subtangent to the curve x2y2=a4 at (−a,a) is
06:38View SolutionThe length of subtangent to the curve, y=ex/a is
05:23View SolutionFind the lengths of subtangent and subnormal at a point on the curve y=bsin(xa)
05:41View SolutionThe length of subtangent to x2y2=a4 at (a,a) is
View SolutionThe length of the subtangent to the curve y2=x22a−x at (a,a) is
01:31View SolutionThe length of the subtangent to the curve x2y2=a4 at any point (−a,a) is
02:36View SolutionThe length of the subtangent at (2, 2) to the cuvre x5=2y4 is
02:36View SolutionThe length of the subtangent of the curve x2+3xy+2y2=0 at (1,2) is
03:55View SolutionThe length of the subtangent at (2, 2) to the curve x5=2y4, is
02:15View Solution
