Find the area of the region in which points satisfy
3≤|x|+|y|≤5.Solution in Bengali
The correct Answer is:32 sq. units
We have 3≤|x|+|y|≤5.
|x|+|y|≤5 means that points lie inside the square endpoints of whose diagonal are (±5,0) and (0,±5).
|x|+|y|≥3 means that points lie outside the square endpoints of whose diagonal are (±3,0) and (0,±3).
So, common region is as shown in the figure.
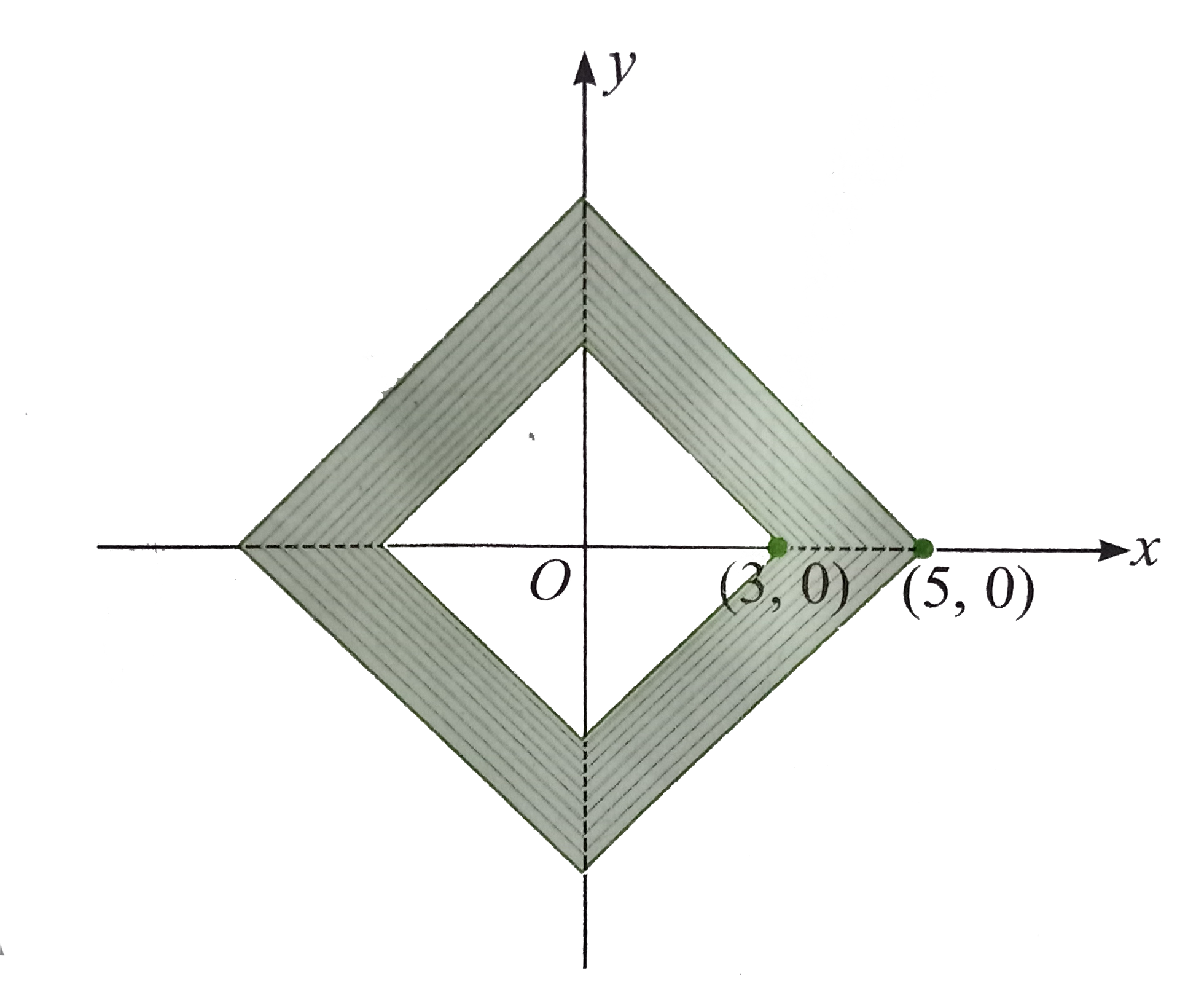
Area of region=4(12×5×5−12×3×3)=32sq.units
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:CONCEPT APPLICATION EXERCISE 2.5
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:CONCEPT APPLICATION EXERCISE 2.6
Explore 5 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:CONCEPT APPLICATION EXERCISE 2.3
Explore 7 Videos
- STRAIGHT LINEBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGE PUBLICATIONChapter:THEORY OF EQUATIONSExercise:JEE ADVANCED (Numerical Value Type )
Explore 1 Video
Similar Questions
Find the equation of the bisector of the obtuse angle between the lines 3x−4y+7=0 and 12x+5y−2=0.
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionFind the points on y−ais whose perpendicular distance from the line 4x−3y−12=0 is 3.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionFind the area of the region formed by x2+y2−6x−4y+12≤0. y≤x and x≤52.
View SolutionFind the area of region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2}.
View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
View SolutionFind the area of the region in which points satisfy
3≤|x|+|y|≤5.
View SolutionFind the area of the region formed by the points satisfying
|x|+|y|+|x+y|≤2.
View SolutionFind the area of the region [x,y):x2+y2≤1≤x+y}
View SolutionFind the area of the region {(x,y):0≤y≤x2,0≤y≤x+2,0≤x≤3}.
View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
View SolutionFind the area of the region in which points satisfy
3≤|x|+|y|≤5.
View SolutionFind the area of the region formed by the points satisfying
|x|+|y|+|x+y|≤2.
View SolutionFind the area bounded by the region given by : A={(x,y):x225+y29≤1≤x5+y3}.
View Solution

