If (a, 3a) is a variable point lying above the straight line 2x+y+4 =0 and below the line x+4y-8=0, then find the values of a. Solution in Bengali
The correct Answer is:
We have lines
Lines are drawn as shown in the following figure.
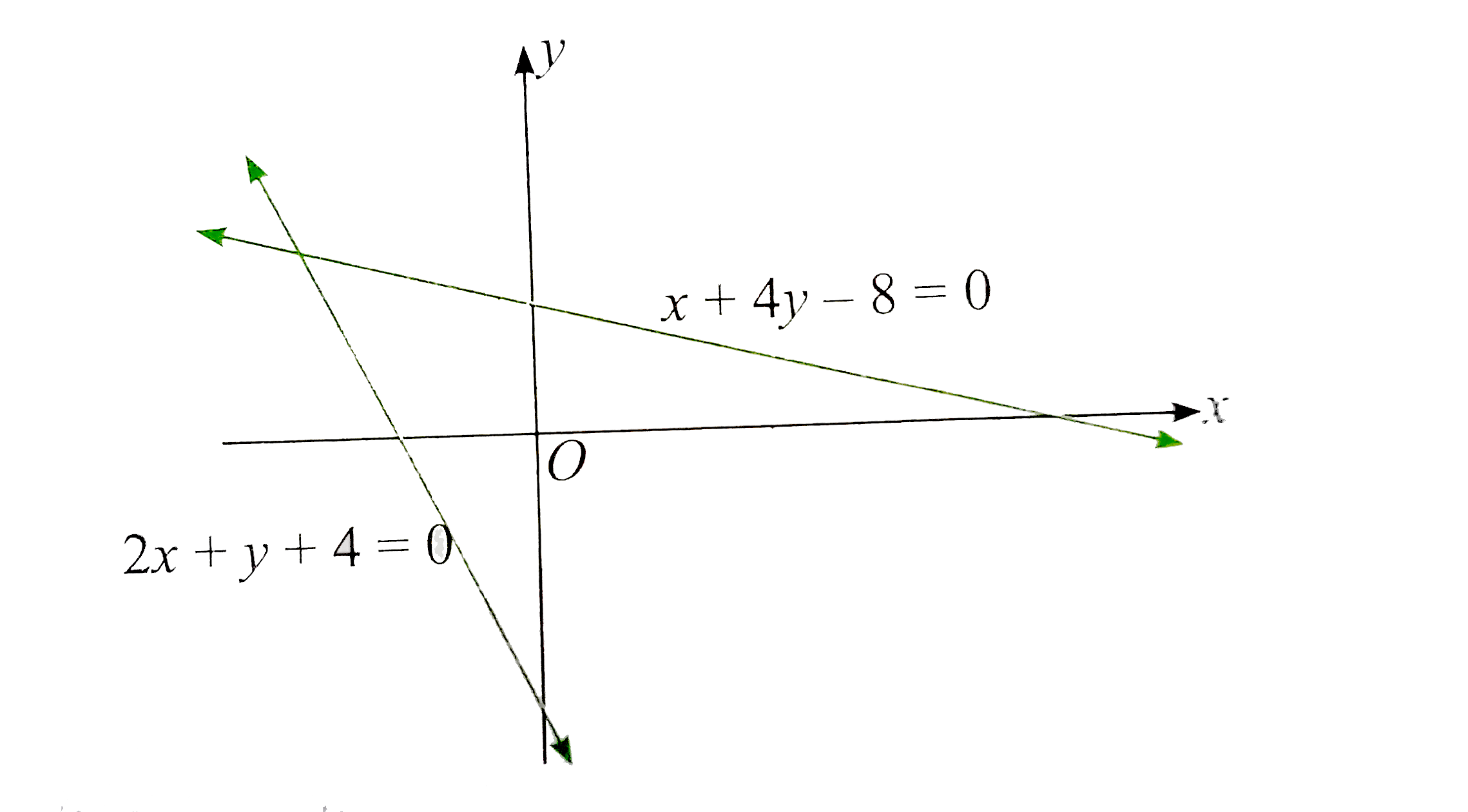
So, (a,3a) lies above the first line if
So, (a,3a) lies below the second line if
From (3) and (4),
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:CONCEPT APPLICATION EXERCISE 2.5
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:CONCEPT APPLICATION EXERCISE 2.6
Explore 5 Videos
- STRAIGHT LINESBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINESExercise:CONCEPT APPLICATION EXERCISE 2.3
Explore 7 Videos
- STRAIGHT LINEBook:CENGAGE PUBLICATIONChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGE PUBLICATIONChapter:THEORY OF EQUATIONSExercise:JEE ADVANCED (Numerical Value Type )
Explore 1 Video
Similar Questions
Find the equation of the bisector of the obtuse angle between the lines 3x−4y+7=0 and 12x+5y−2=0.
View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
View SolutionFind the points on y−ais whose perpendicular distance from the line 4x−3y−12=0 is 3.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionDistance of a point (2,5) from the line 2x-y-4=0 measured parallel to the line 3x-4y+8=0 is :
View SolutionOn the straight line y=x+2, a point (a,b) is such that the sum of the square of the distances from the straight lines 3x-4y+8=0 and 3x-y-1=0 is least then find value of 11(a+b)
View SolutionIf (a, 3a) is a variable point lying above the straight line 2x+y+4 =0 and below the line x+4y-8=0, then find the values of a.
View SolutionIf the straight line ax+y+6=0 passes through the point of intersection of the lines x+y+4=0and2x+3y+10=0, find a.
View SolutionFind the equation of the straight line passing through the point of intersection of the straight lines x+2y+3=0 and 3x+4y+7=0 and parallel to the straight line y=−58x.
View SolutionIf the straight line xa+yb=1 is parallel to the line 4x + 3y = 6 and passes through the point of intersection of the lines 2x - y - 1 = 0 and 3x - 4y + 6 = 0 ,find the values of a and b .
View Solutiona का मान ज्ञात कीजिए जबकि सरल रेखा 2x+y+5+a(x+y)=0 :
रेखा 3x+4y=5 पर लम्ब हो ।
View Solutionउस सरल रेखा का समीकरण निकालें जो सरल रेखाओं x+2y+3=0 तथा 3x+4y+7=0 के छेदन-बिंदु से जाती है तथा सरल रेखा y−x=8 पर लम्ब है।
View SolutionFind the value of a if the distances of the points (2,3) and (−4,a) from the straight line 3x+4y−8=0 are equal.
View Solutionउस सरल रेखा का समीकरण ज्ञात कीजिए जो सरल रेखाओं 2x+3y+4=0 और 3x+4y−5=0
की प्रतिच्छेद-बिन्दु से होकर जाती है और सरल रेखा 6x−7y+8=0 पर लम्ब है।
View SolutionThe perpendicular distance of the straight line 3x + 4y- 8 = 0 from the point of intersection of the lines 3x + 2y + 4 = 0, 2x + 5y -1=0 is
View Solution

