Evaluate : [limx→0sinxx], where [⋅] represents the greatest integer function.Solution in Bengali
See the graphs of y=x and sinx in the following figure.
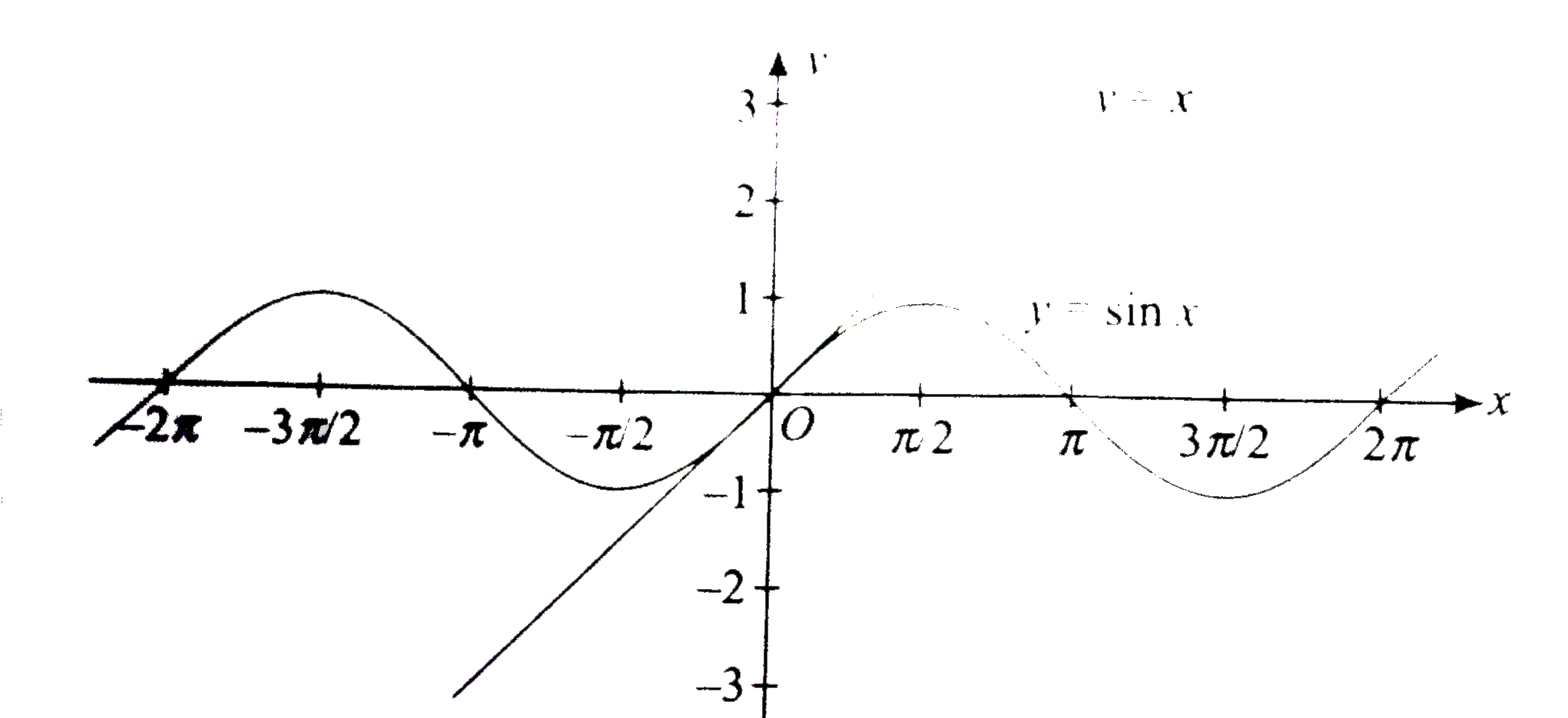
From the figure when x→0+,graph of y=x is above the graph of y=sinx
i.e., sinx<x or sinxx<1
⇒ limx→0+sinxx=11−
⇒ [limx→0+sinxx]=0
When x→0−, graph of y=x is below the graph of y=sinx
i.e., sinx<x or sinxx<1 (as x is negative)
⇒ limx→0−sinxx=1−
⇒ [limx→0−sinxx]=0
Thus, [limx→0−sinxx]=0
Topper's Solved these Questions
- LIMITSBOOK - CENGAGE PUBLICATIONCHAPTER - LIMITSEXERCISE - Solved Examples
15 Videos
- LIMITSBOOK - CENGAGE PUBLICATIONCHAPTER - LIMITSEXERCISE - EXERCISE 2.1
10 Videos
- JEE 2019BOOK - CENGAGE PUBLICATIONCHAPTER - JEE 2019EXERCISE - Chapter 10
8 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBOOK - CENGAGE PUBLICATIONCHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.2
10 Videos
Similar Questions
Evaluate:limn→∞n2⎧⎪ ⎪⎨⎪ ⎪⎩ ⎷(1−cos(1n)) ⎷(1−cos(1n))√(1−cos(1n))..∞⎫⎪ ⎪⎬⎪ ⎪⎭.
View SolutionEvaluate limx→−2+x2−12x+4.
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionThe number of integral values of p for which (p+1)ˆi−3ˆj+pˆk,pˆi+(p+1)ˆj−3ˆk and −3ˆi+pˆj+(p+1)ˆk are linearly dependent vectors is q
View SolutionEvaluate: (lim)x→0sinxx,where[.] represents the greatest integer function.
View SolutionEvaluate: [(lim)x→0tan−1xx], where [.]represent the greatest integer function
View SolutionEvaluate: (lim)x→0tanxx where [.] represents the greatest integer function
View SolutionEvaluate : (lim)x→2+ [x−2]log(x−2) , where [.] represents the greatest integer function.
View SolutionEvaluate: (lim)x→0 sin[cosx]1+[cosx]([.] denotes the greatest integer function).
View SolutionEvaluate : [limx→0sinxx], where [⋅] represents the greatest integer function.
View SolutionFind the domain and range of f(x)=sin−1(x−[x]), where [.] represents the greatest integer function.
View SolutionEvaluate limx→0[sin−1xx] ( where [∗] denotes the greatest integer function ) .
View Solutionlimx→0[(1−ex)sinx|x|] is equal to
( where [∗]denotes greatest integer function )
View SolutionEvaluate: [(lim)x→0tan−1xx], where [.]represent the greatest integer function
View SolutionEvaluate : (lim)x→2+ [x−2]log(x−2) , where [.] represents the greatest integer function.
View SolutionEvaluate : [limx→0sinxx], where [⋅] represents the greatest integer function.
View Solution
