Let and be respectively given by . Define by
The number of points at which is not differentiable isSolution in Bengali
First we draw the graph, of
is a parabola having vertex at (0, 1) and concave upwards
Thus, the graphs of both functions are as shown in the following figure.
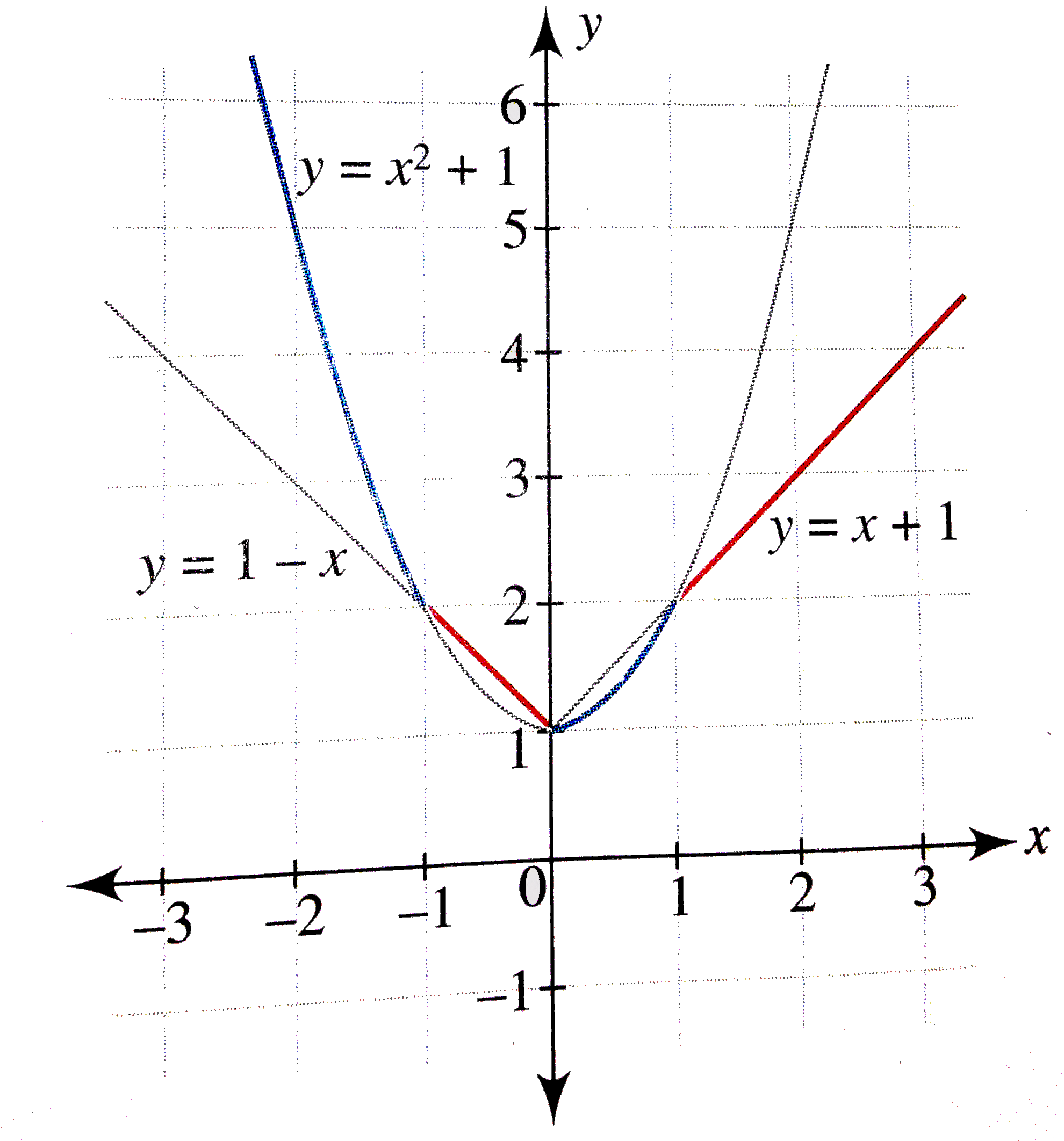
From the graph, the required function is
which is non-different at .
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGE PUBLICATIONChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:EXERCISES
Explore 34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGE PUBLICATIONChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercises
Explore 17 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGE PUBLICATIONChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercises
Explore 22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionDraw the graph of y=(x−1)(x2−x+1).
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet f:R rarr R and g:R rarr R be respectively given by f(x)=|x|+1 and g(x)=x^(2)+1. Define h:R rarr R by h(x)={max{f(x),g(x)},quad if x 0 The number of points at which h(x) is not differentiable is
View SolutionLet f(x)={x-1,-1<=x<0 and x^(2),0<=x<=1,g(x)=sin x and h(x)=f(|g(x)|)+[f(g(x)) Then
View SolutionLet the function f, g, h are defined from the set of real numbers RR to RR such that f(x) = x^2-1, g(x) = sqrt(x^2+1), h(x) = {(0, if x lt 0), (x, if x gt= 0):}. Then h o (f o g)(x) is defined by
View SolutionLet f(x)=f1(x)−2f2(x), where
where f(x)={min{x2,|x|},|x|≤1max{x2,|x|},|x|>1
and f2(x)={min{x2,|x|},|x|>1max{x2,|x|},|x|≤1
and let g(x)={min{f(t):−3≤t≤x, −3≤x<0}max{f(t):0≤t≤x, 0≤x≤3}
For x∈(−1,0),f(x)+g(x) is
View SolutionLet f be a twice differentiable function such that
f''(x)=−f(x) and f'(x)=g(x).If h'(x)=[f(x)]2+[g(x)]2,
h(a)=8 and h(0)=2, then h(2)=
View SolutionLet f:R→R and g:R→R be respectively given by f(x)=|x|+1 and g(x)=x2+1. Define h:R→R by
h(x)={max{f(x),g(x)}ifx≤0min{f(x),g(x)}ifx>0
The number of points at which h(x) is not differentiable is :
View SolutionLet f:R→R be defined by f(x)=−x3+x,g:[−1,1]→Randh:[−1,1]→R is defined by g(x) = min(fx),0), h(x) = max(f(x),0)
Number of roots of the g(x)=−12 is____
View SolutionLet f(x) ={x+1:x£0x:x>0 and h (x) = |f(x) + f(|x|) . Then h(x) is defined by :
View Solutionমনে করাে, f:R→R হল f(x)=−x3+x দ্বারা সংজ্ঞাত। g:[−1,1]→R,h:[−1,1]→R নিম্নরূপে সংজ্ঞাত। g(x)=min(f(x),0),h(x)=max(f(x),0) : g(x) এর পাল্লা হয় -
View Solutionমনে করাে, f:R→R হল f(x)=−x3+x দ্বারা সংজ্ঞাত। g:[−1,1]→R,h:[−1,1]→R নিম্নরূপে সংজ্ঞাত। g(x)=min(f(x),0),h(x)=max(f(x),0) :g(x)=−12 সমীকরণের বীজসংখ্যা হয় -
View Solutionমনে করাে, f:R→R হল f(x)=−x3+x দ্বারা সংজ্ঞাত। g:[−1,1]→R,h:[−1,1]→R নিম্নরূপে সংজ্ঞাত। g(x)=min(f(x),0),h(x)=max(f(x),0) : নীচের কোনটি যুগ এবং অযুগ্ম উভয় অপেক্ষকই?
View SolutionIf f(x)=(g(x))+g(−x)2+2[h(x)+h(−x)]−1 where g and h are differentiable functions then f'(0)
View SolutionLet f(x) be defined on [−2,2] and be given by f(x)={−1;−2≤x≤0} andf(x)={x−1;0<x≤2}.andg(x)=f(|x|)+|f(x)| Find g(x)
View Solution