If b>a, then the equation (x−a)(x−b)−1=0 has
(a) Both roots in (a,b) (b) Both roots in (−∞,a)
(c) Both roots in (b,+∞) (d) One root in (−∞,a) and the other in (b,+∞) Solution in Bengali
Given equation is (x−a)(x−b)−1=0
Let f(x)=(x−a)(x−b)−1
f(a)=−1
and f(b)=−1
Graph of f(x) is concave upwards, hence aandb lie between the roots.
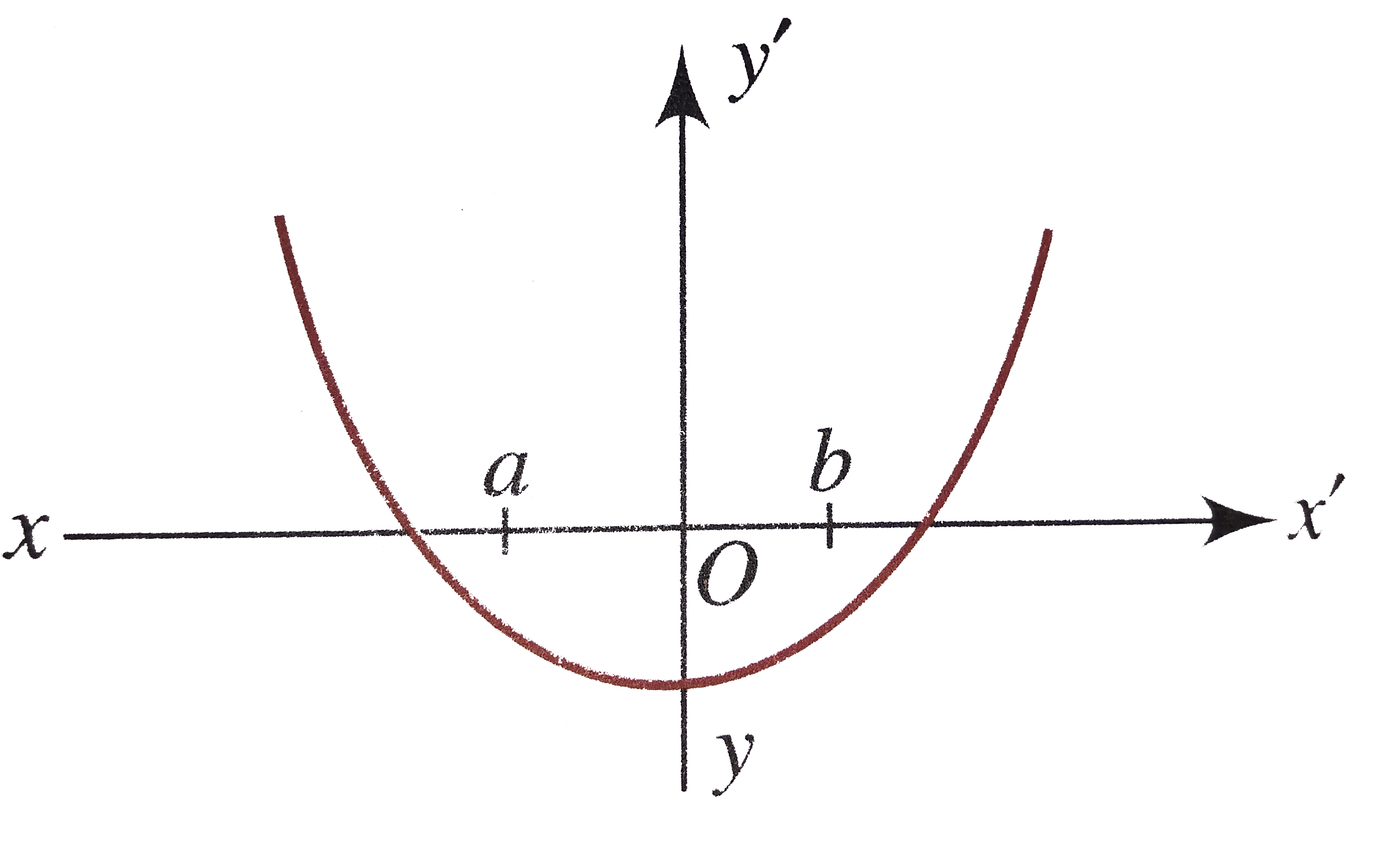
Also b>a, then one root is in (−∞,a) and the other is in (b,+∞).
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionDraw the graph of y=(x−1)(x2−x+1).
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionIf b>a, then the equation (x−a)(x−b)−1=0 has (a) both roots in (a,b) (b) both roots in (−∞,a) (c) both roots in (b,+∞) (d)one root in (−∞,a) and the other in (b,+∞)
View SolutionThe range of a for which the equation x2+ax−4=0 has its smaller root in the interval (−1,2)is a. (−∞,−3) b. (0,3) c. (0,∞) d. (−∞,−3)∪(0,∞)
View SolutionIf b>a, then the equation (x−a)(x−b)−1=0 has (2000,1M) both roots in (a,b) both roots in (−∞,a) both roots in (b,+∞) one root in (−∞,a) and the other in (b,∞)
View SolutionIf the equation x3−12x+a=0 has exactly one real root, then range of a is equal to (−∞, −16)∪(16, ∞) (b) {−16, 16} (−16, 16) (d) (−∞, −16)∪[16, ∞)
View SolutionConsider the quadratic equationx2−mx+1=0 with two roots αand β such that α+β=m and αβ=1 The value of m for which both the roots of the equation are less than unity are (A) ]−∞,−2] (B) [−2,2] (C) [2,∞] (D) ]−∞,−2]∪[2,∞]
View SolutionIf 0<α<π4 equation (x−sinα)(x−cosα)−2=0 has (A) both roots in (sinα,cosα) (B) both roots in (cosα,sinα) (C) one root in (−∞,cosα) and other in (sinα,∞) (D) one root in (−∞,sinα) and other in (cosα,∞)
View SolutionThe set of all values of a for which both roots of equation x2−ax+1=0 are less than unity is (A) (−∞,−2) (B) (−2,∞) (C) (−2,3) (D) (−∞,−1)
View SolutionIf b>a, then the equation (x−a)(x−b)−1=0 has
(a) Both roots in (a,b) (b) Both roots in (−∞,a)
(c) Both roots in (b,+∞) (d) One root in (−∞,a) and the other in (b,+∞)
View SolutionEvaluate : (a) √x√x√x.....∞ (b) √6+√6+√6+......∞
(c) √a33√b√a33√b.......∞
View SolutionFor the quadratic equatio x2−(k−3)x+k=0 , match the condition in condition in column I with the correspending values of k in column II.
{:("Column-I " , " Column -II"),("(A) Both the roots are positive", "(p) " phi),("(B) Both the roots are negative " , "(q) " (-oo","1) cup (9","oo)),("(C) Both the roots are real " , "(r) " [10 "," oo)),(" (D) one root is less than -1 and other is greater than 1" "(s) " (0","1]),(" " , "(t) " [ 125"," 1250]):}
View SolutionIf b>a, then the equation (x−a)(x−b)−1=0 has (a) both roots in (a,b) (b) both roots in (−∞,a) (c) both roots in (b,+∞) (d)one root in (−∞,a) and the other in (b,+∞)
View SolutionIf a,b,c∈R and abc<0 , then equation bcx2+(2b+c−a)x+a=0 has (a). both positive roots (b). both negative roots (c). real roots (d) one positive and one negative root
View SolutionIf b>a, then the equation (x−a)(x−b)−1=0 has
(a) Both roots in (a,b) (b) Both roots in (−∞,a)
(c) Both roots in (b,+∞) (d) One root in (−∞,a) and the other in (b,+∞)
View Solution
