The diagram shows the graph of the derivative of a function f(x) for with f(0) = 0. Which of the following could be correct statements for y = f(x)?
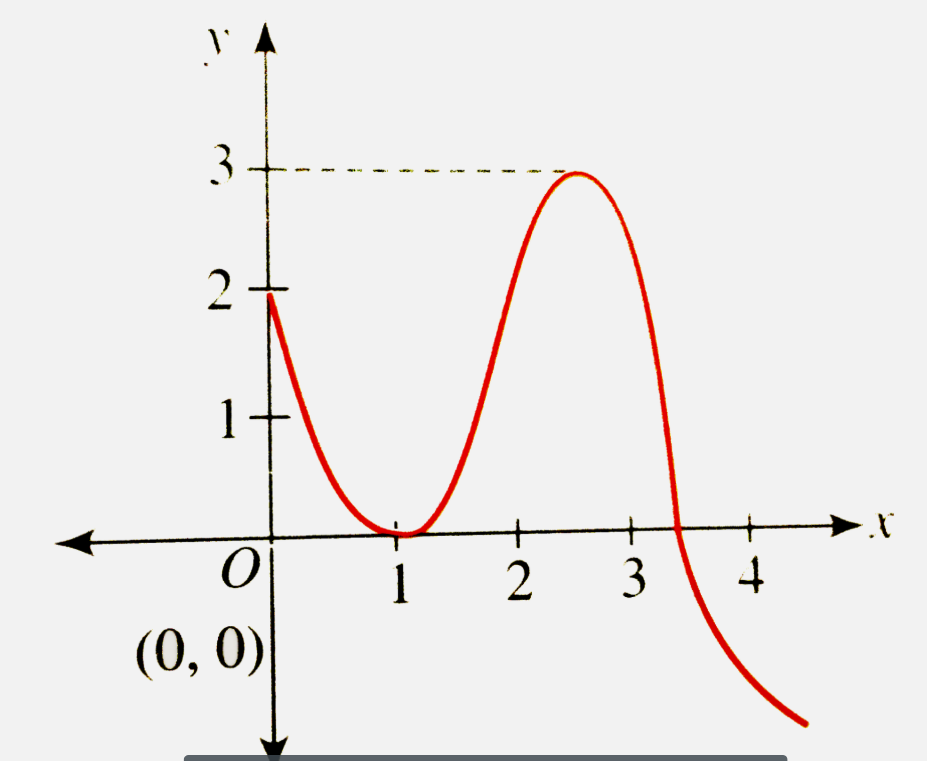
(a) Tangent line to y = f(x) at x = 0 makes an angle of with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two. Solution in Bengali
Slope of y tangent at .
Hence (a) is correct.
, hence f is increasing for (0, 3) , and so (b) is correct.
The x - axis is tangent to the curve at x = 1, therefore f''(1) = 0.
So x = 1 is point of inflection, but not the point of extremum as the sign of f'(x) does not change at x = 1.
Hence (c) is not correct.
Obviously, y = f(x) has two critical points as f'(1) = 0 and f'(3.5) = 0.
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.22
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.23
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.20
1 Videos
- FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
18 Videos
Similar Questions
In the following graph, state the absolute and local maximum and minimum values of the function.
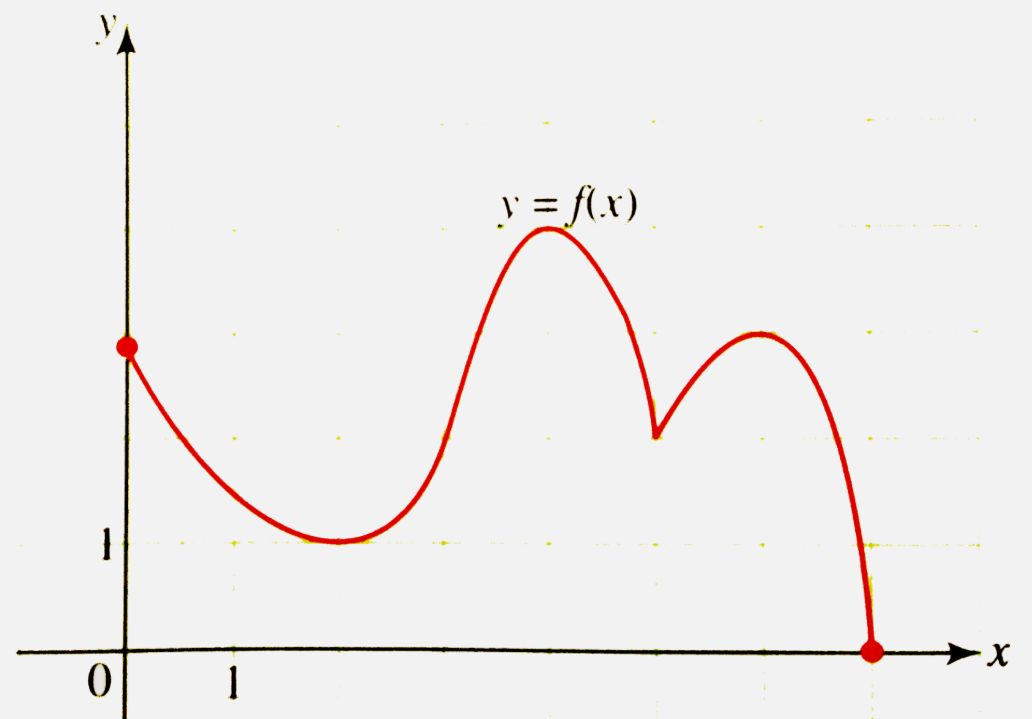
View SolutionThe graph of the derivative f'(x) is given in the following figure.
(b) Find the values of x for which f has local maximum or minimum.
(c) Find the intervals in which f is concave upward or downward.
(d) Find the point of inflection.

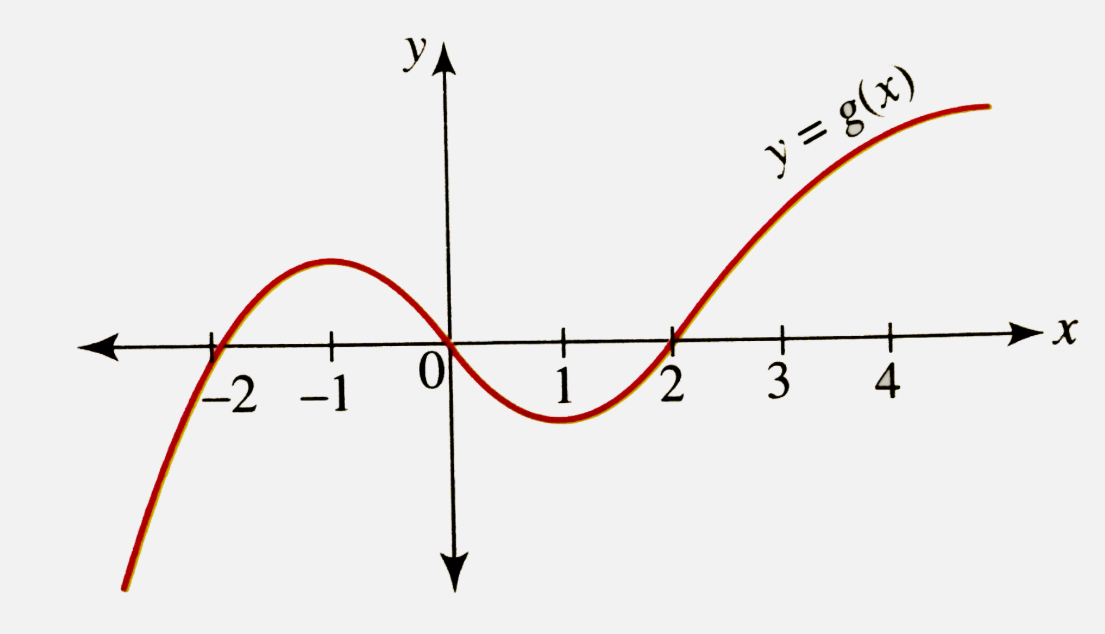
View SolutionFor the function g whose graph is given. Arrange the following numbers in increasing order and explain your reasoning.
g(0),g'(−2),g'(0),g'(2),g'(4)
View SolutionLet f(x)=x2−2x−1∀x∈R.Letf:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective.
If f:R→R, then range of values of k for which equation f(|x|)=k has 4 distinct real roots is
View SolutionDraw the graph of y=tan−1x−cot−1x.
View SolutionLet y = f(x) be a function such that f(x)=x3 and the line x + y = 0 is tangent to the graph of f(x) then which of the following alternative(s) is/are correct? f(0)=−34 (b) f (1)=1 f(−1)=1 (d) f(3)=21
View Solutiony=f(x) is a function which satisfies f(0)=0, f"''(x)=f'(x) and f'(0)=1 then the area bounded by the graph of y=f(x) , the lines x=0, x-1=0 and y+1=0 is
View SolutionFollowing is the graph of y = f(x).
(##CENGRAC01S01005_Q01.png width=80%><br>F∈dthes√oftheequation f(x) = 0, f(x) = 4 and f(x) = 10.
View SolutionThe diagram shows the graph of the derivative of a functin f(x) for 0≤x≤4 with f(0) = 0. Which of the following could be correct statements for y = f(x)?
(##CENGRAC01S01021_Q01.png width=80%><br>(a)Tan≥ntl∈e→y=f(x)atx=0makesan∠of sec^(-1) sqrt 5 with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two.
View SolutionAt x=0, value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_024_Q01.png" width="80%"gt
View SolutionSuppose f:[−2,2]→R is defined by f(x)={−1 for −2≤x≤0x−1 for 0≤x≤2 , then {x∈[−2,2]:x≤0andf(|x|)=x}=
View SolutionIf f(x)=x2, if 0≤x≤1 =√x, if x≥1,
then area above X-axis, bounded by the line x = 4 and the curve y = f(x) is
View SolutionIf f(x)=|x−3|+|x−4|, then in the interval 0≤x≤5, the function f(x) is -
View SolutionA function y=f(x) is defined as follows :
y=f(x)={x2 when 0≤x≤1√x when x≥1
Then the area ( in square unit ) above the x- axis included between the curve y= f(x) and the line x = 4 is-
View SolutionIf f(x) is a differentiable function satisfying |f'(x)|≤2∀x∈[0,4] and f(0)=0, then
View SolutionDraw the graph of the function f(x)={1+x−1≤x≤01−x0<x≤1
View Solution
