For what values of p and q the system of equations 2x+py+6z=8,x+2y+qz=5,x+y+3z=4 has (i) no solution (ii) a unique solution (iii) in finitely many solutions.Solution in Bengali
p=2,q∈3
p∈2,q∈3
p≠2,q=3
p=2,q=3
The correct Answer is:b
The given system of equations is
2x+py+6z=8
x+2y+qz=5
x+y+3z=4
Δ=∣∣
∣
∣∣2p612q113∣∣
∣
∣∣=(2−p)(3−q)
By Cramer's rule, if Δ≠0, i.e., p≠2andq≠3, the system has a unique solution.
If p=2orq=3,Δ=0, then if Δx=Δy=Δz=0, the system has infinite solutions and if any one of Δx,ΔyandΔz≠0, the system has no solution.
Now Δx=∣∣
∣
∣∣8p652q413∣∣
∣
∣∣
=30−8q−15p+4pq=(4q−15)⋅(p−2)
Δy=∣∣
∣
∣∣28615q143∣∣
∣
∣∣
=−8q+8q=0
Δz=∣∣
∣
∣∣2p8125114∣∣
∣
∣∣
Thus, if p=2,Δx=Δy=Δz=0 for all q∈R, the system has infinite solutions.
If p≠2,q=3andΔz≠0, then the system has no solutions.
Hence the system has (i) no solution if p≠2andq=3, (ii) a unique solution if p≠2andq≠3 and (iii) infinite solutions of p=2andq∈R.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - INTEGER TYPE10videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - REASONING TYPE10videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
Similar Questions
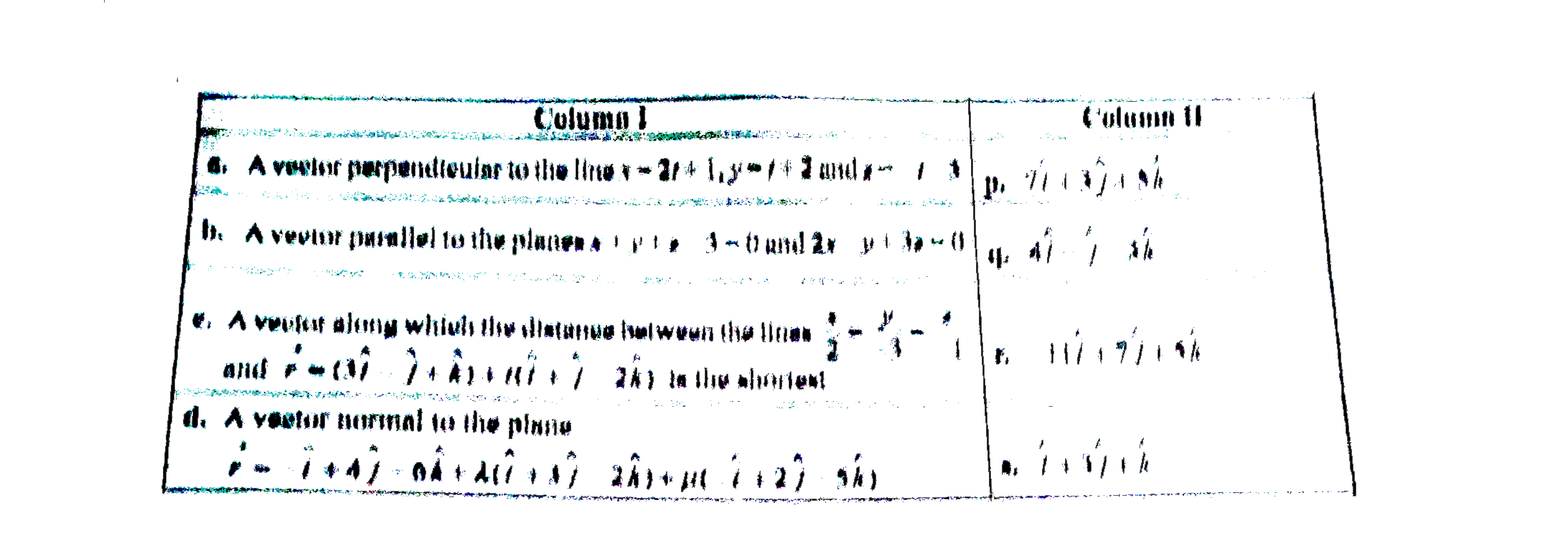 03:38View Solution
03:38View SolutionFind the number of sphere of radius r touching the coordinate axes.
06:11View SolutionStatement 1: Lines →r=ˆi+ˆj−ˆk+λ(3ˆi−ˆj)and→r=4ˆi−ˆk+μ(2ˆi+3ˆk) intersect. Statement 2: →b×→d=0 , then lines →r=→a+λ→band→r=→c+λ→d do not intersect.
07:07View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
02:49View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
02:55View SolutionFor what values of aandb, the system of equations 2x+ay+6z=8 x+2y+bz=5 x+y+3z=4 has: (i) a unique solution (ii) infinitely many solutions no solution
05:13View SolutionFor what values of p and q the system of equations 2x+py+6z=8,x+2y+qz=5,x+y+3z=4 has (i) no solution (ii) a unique solution (iii) in finitely many solutions.
09:34View Solutionमान लीजिए 2x+py+6z=8,x+2y+qz=5 तथाx+y+3z=4 समीकरण निकाय है ।
समीकरण निकाय का कोई हल नहीं है , यदि09:10View Solutionमान लीजिए 2x+py+6z=8,x+2y+qz=5 तथाx+y+3z=4 समीकरण निकाय है ।
समीकरण का अद्वितीय हल होगा , यदि14:15View Solutionमान लीजिए 2x+py+6z=8,x+2y+qz=5 तथाx+y+3z=4 समीकरण निकाय है ।
समीकरण निकाय के अनंत हल होंगे , यदि02:55View Solution" The system of equations "2x+py+6z=8,x+2y+qz=5,x+y+3z=4" will have no solution if "
06:30View SolutionFor what values of p and q the system of equations 2x+py+6z=8,x+2y+qz=5,x+y+3z=4 has i no solution ii a unique solution iii in finitely many solutions.
12:05View SolutionFor what values of p and q the system of equations 2x+py+6z=8,x+2y+qz=5,x+y+3z=4 has i no solution ii a unique solution iii in finitely many solutions.
06:11View SolutionFor what values of a and b, the system of equations 2x+ay+6z=8, x+2y+bz=5, x+y+3z=4 has: (i) a unique solution (ii) infinitely many solutions (iii) no solution
05:17View SolutionFor what values of p and q the system of equations 2x+py+6z=8,x+2y+qz=5,x+y+3z=4 has i no solution ii a unique solution iii in finitely many solutions.
07:14View SolutionFor what values of p and q the system of equations 2x+py+6z=8,x+2y+qz=5,x+y+3z=4 has (i) no solution (ii) a unique solution (iii) in finitely many solutions.
03:55View Solution
