For what values of p and q the system of equations has (i) no solution (ii) a unique solution (iii) in finitely many solutions.Solution in Bengali
1..
2.
3.
4.
The correct Answer is:b
The given system of equations is
By Cramer's rule, if , i.e., , the system has a unique solution.
If , then if , the system has infinite solutions and if any one of , the system has no solution.
Now
Thus, if for all , the system has infinite solutions.
If , then the system has no solutions.
Hence the system has (i) no solution if , (ii) a unique solution if and (iii) infinite solutions of .
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY Book:CENGAGE PUBLICATIONChapter:THREE-DIMENSIONAL GEOMETRY Exercise:MATRIX-MATCH TYPE
Explore 5 Videos
- THREE-DIMENSIONAL GEOMETRY Book:CENGAGE PUBLICATIONChapter:THREE-DIMENSIONAL GEOMETRY Exercise:INTEGER TYPE
Explore 10 Videos
- THREE-DIMENSIONAL GEOMETRY Book:CENGAGE PUBLICATIONChapter:THREE-DIMENSIONAL GEOMETRY Exercise:REASONING TYPE
Explore 10 Videos
- THREE DIMENSIONAL GEOMETRYBook:CENGAGE PUBLICATIONChapter:THREE DIMENSIONAL GEOMETRYExercise:All Questions
Explore 291 Videos
- TRIGONOMETRIC EQUATIONSBook:CENGAGE PUBLICATIONChapter:TRIGONOMETRIC EQUATIONSExercise:Archives (Numerical value type)
Explore 4 Videos
Similar Questions
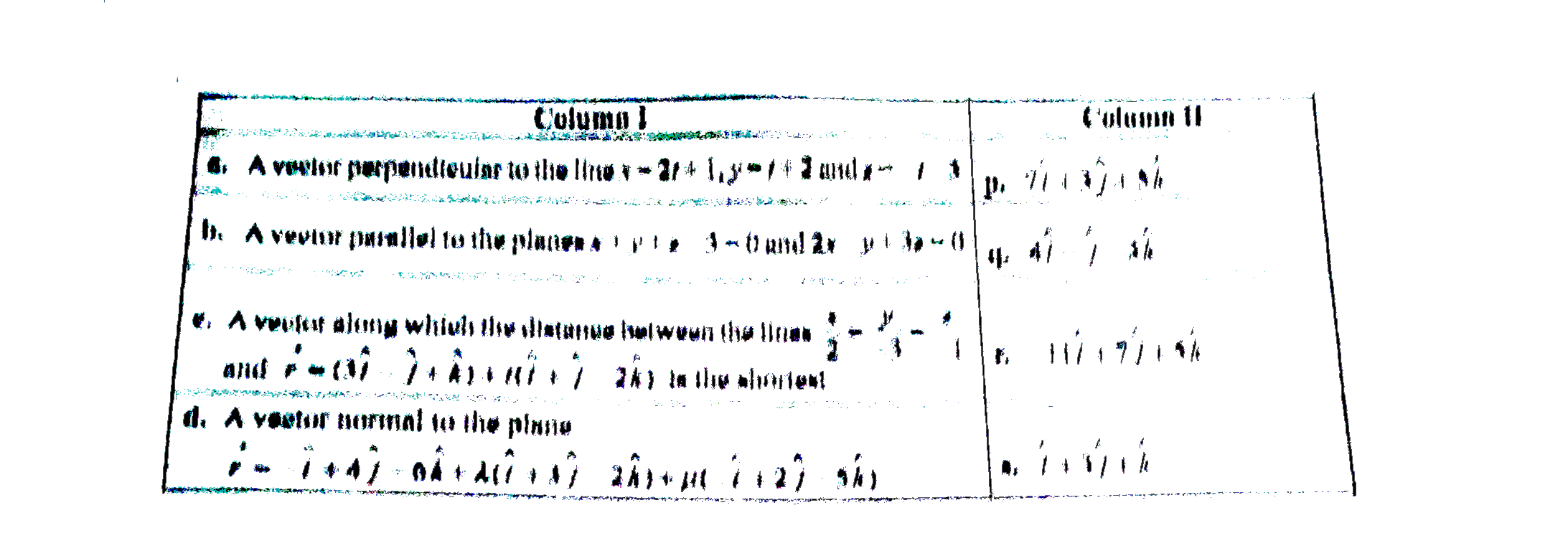
View SolutionFind the number of sphere of radius r touching the coordinate axes.
View SolutionStatement 1: Lines →r=ˆi+ˆj−ˆk+λ(3ˆi−ˆj)and→r=4ˆi−ˆk+μ(2ˆi+3ˆk) intersect. Statement 2: →b×→d=0 , then lines →r=→a+λ→band→r=→c+λ→d do not intersect.
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
View SolutionFor what values of aandb, the system of equations 2x+ay+6z=8 x+2y+bz=5 x+y+3z=4 has: (i) a unique solution (ii) infinitely many solutions no solution
View Solutionमान लीजिए 2x+py+6z=8,x+2y+qz=5 तथाx+y+3z=4 समीकरण निकाय है ।
समीकरण निकाय का कोई हल नहीं है , यदि
View Solutionमान लीजिए 2x+py+6z=8,x+2y+qz=5 तथाx+y+3z=4 समीकरण निकाय है ।
समीकरण का अद्वितीय हल होगा , यदि
View Solutionमान लीजिए 2x+py+6z=8,x+2y+qz=5 तथाx+y+3z=4 समीकरण निकाय है ।
समीकरण निकाय के अनंत हल होंगे , यदि
View SolutionConsider three planes, 2x+py+6z=8,x+2y+qz=5andx+y+3z=4.
View SolutionConsider the system of equations
2x+λy+6z=8x+2y+μz=5x+y+3z=4
The system of equations has :
No solution if :
View Solution" The system of equations "2x+py+6z=8,x+2y+qz=5,x+y+3z=4" will have no solution if "
View SolutionIf the system of equations 2x+ay+6z=8, x+2y+z=5, 2x+ay+3z=4 has a unique solution then 'a' cannot be equal to :
View SolutionFor what values of aandb, the system of equations 2x+ay+6z=8 x+2y+bz=5 x+y+3z=4 has: (i) a unique solution (ii) infinitely many solutions no solution
View SolutionFor what values of a and b, the system of equations 2x+ay+6z=8, x+2y+bz=5, x+y+3z=4 has: (i) a unique solution (ii) infinitely many solutions (iii) no solution
View Solution. For what values of λ and μ the system of equations x+y+z=6,x+2y+3z=10,x+2y+λz=μ has (i) Unique solution (ii) No solution (iii) Infinite number of solutions
View Solution
