Statement 1: Line x−11=y−02=z+2−1 lies in the plane 2x−3y−4z−10=0. Statement 2: if line →r=→a+λ→b lies in the plane →r.→c=n (where n is scalar),then →b.→c=0. (a) Both the statements are true, and Statement 2 is the correct explanation for Statement 1. (b) Both the Statements are true, but Statement 2 is not the correct explanation for Statement 1. (c)Statement 1 is true and Statement 2 is false. (d) Statement 1 is false and Statement 2 is true. Solution in Bengali
Both the statements are true, and Statement 2 is the correct explanation for Statement 1.
Both the Statements are true, but Statement 2 is not the correct explanation for Statement 1.
Statement 1 is true and Statement 2 is false.
Statement 1 is false and Statement 2 is true.
The correct Answer is:c
Statement 2 is true as when the line lies in the plane, vector →b along which the line is directed is perpendicular to the normal →c of the plane, but it does not explain Statement 1 as for →b⋅→c=0, the line may be parallel to the plane. However, Statement 1 is correct as any point on the line (t+1,2t,−t−2) lies on the plane for t∈R.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - LINKED COMPREHENSION TYPE12videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CORRECT ANSWER TYPE17videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
Similar Questions
Given four points A(2,1,0),B(1,0,1),C(3,0,1)andD(0,0,2). Point D lies on a line L orthogonal to the plane determined by the points A, B and C.
The equation of the plane ABC is04:53View Solution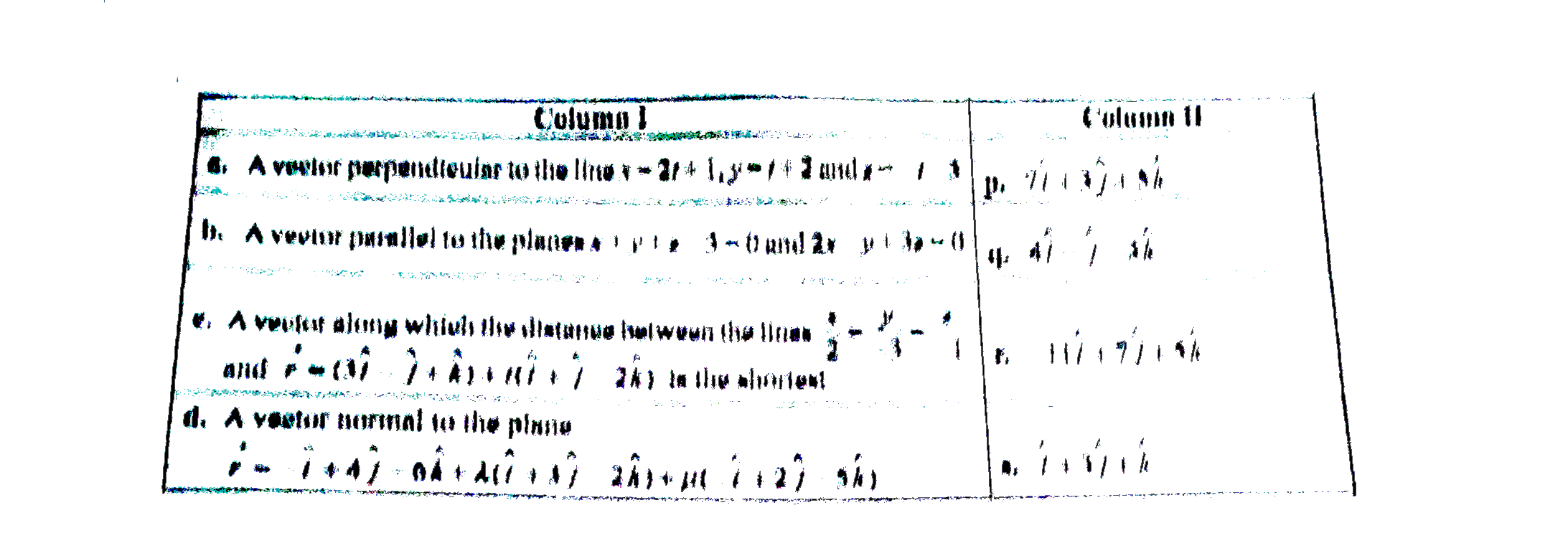
02:27View SolutionLet PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle φ with the positive direction of x− axis, whereO is the origin and θandφ are acute angels, then a. cosθcosφ=1/√14 b. sinθsinφ=2/√14 c. tanφ=2 d. tanθ=√5/3
02:29View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
01:55View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
04:47View SolutionStatement 1: Line x−11=y−02=z2−1 lies in the plane 2x−3y−4z−10=0. Statement 2: if line →r=→a+λ→b lies in the plane →r.→c=n(wheren is scalar),then→b.→c=0.
01:15View SolutionStatement 1: In ΔABC,−−→AB+−−→BC+−−→CA=0
Statement 2: If −−→OA=→a,−−→OB=→b,then −−→AB=→a+→b05:45View SolutionStatement 1: If ∣∣→a+→b∣∣=∣∣→a−→b∣∣, then →a and →b are perpendicular to each other. Statement 2: If the diagonal of a parallelogram are equal magnitude, then the parallelogram is a rectangle. Which of the following Statements is/are correct ?
05:03View SolutionStatement 1: Line x−11=y−02=z2−1 lies in the plane 2x−3y−4z−10=0. Statement 2: if line →r=→a+λ→b lies in the plane →r.→c=n(wheren is scalar),then→b.→c=0.
03:30View SolutionStatement 1: Line x−11=y−02=z+2−1 lies in the plane 2x−3y−4z−10=0. Statement 2: if line →r=→a+λ→b lies in the plane →r.→c=n(wheren is scalar),then→b.→c=0.
06:39View SolutionStatement 1: In DeltaABC,→AB+→AB+→CA=0 Statement 2: If →OA=→a,→OB=→b,then→AB=→a+→b
01:56View Solutionकथन-1 : यदि →r त्रिविम में कोई सदिश हो, तो
→r=(→r.ˆi)ˆi+(→r.ˆj)ˆj+(→r.ˆk)ˆk
कथन-2 : यदि →a,→b,→c तीन असमतलीय सदिश त्रिविम में है तथा त्रिविम में कोई सदिश →r है, तो
→r={→r.→a|→a|2}→a+⎧⎪⎨⎪⎩→r.→b∣∣→b∣∣2⎫⎪⎬⎪⎭→b+{→r.→c|→c|2}→c02:46View SolutionStatement 1: In DeltaABC,→AB+→BC+→CA=0 Statement 2: If →OA=→a,→OB=→b,then→AB=→a+→b
02:37View SolutionLet →r be a non-zero vector satisfying →r.→a=→r.→b=→r.→c=0 for given non-zero vectors →a,→band→⋅ Statement 1: [→a−→b→b−→c→c−→a]=0 Statement 2: [→a→b→c]=0
03:49View SolutionStatement 1: If vec A=2 hat i+3 hat j+6 hat k , vec B= hat i+ hat j-2 hat ka n d vec C= hat i+2 hat j+ hat k , then | vec Axx( vec Axx( vec Axx vec B)). vec C|=243 Statement 2: | vec Axx( vec Axx( vec Axx vec B)). vec C|=| vec A|^2|[ vec A vec B vec C]| a. Statement 1 and Statement 2 , both are true and Statement 2 is the correct explanation for Statement 1. b. Statement 1 and Statement 2 , both are true and Statement 2 is not the correct explanation for Statement 1. c. Statement 1 is true but Statement 2 is false. c. Statement 2 is true but Statement 1 is false.
06:05View SolutionStatement 1: Line x−11=y−02=z2−1 lies in the plane 2x−3y−4z−10=0. Statement 2: if line →r=→a+λ→b lies in the plane →r.→c=n(wheren is scalar),then→b.→c=0.
07:25View Solution