आरम्भिक वेग →v=v0ˆi(v0>0) और द्रव्यमान m का कोई इलेक्ट्रॉन किसी वैधुत क्षेत्र →E=−E0ˆi (E0= स्थिरांक >0 ) में t= 0 पर प्रवेश करता है । यदि प्रारम्भ में इस इलेक्ट्रॉन की दी-ब्रोगली तरंगदैर्घ्य λ0 है , तो समय t पर इसकी दी-ब्रोगली तरंगदैर्घ्य होगी :
λ0t
λ0(1+eE0mV0t)
λ0(1+eE0mV0t)
λ0
The correct Answer is:C
आरम्भिक दे-ब्रॉग्ली तरंगदैर्ध्य
λ0=hmV0 ....(i)

इलेक्ट्रॉन का त्वरण
a=eE0m (∵F=ma=eE0)
t समय पश्चात, वेग
V=(V0+eE0mt)
अतः λ=hmV=hm(V0+eE0mt)
=hmV0[1+eE0mV0t]=λ0[1+eE0mV0t] ....(ii)
समी. (ii) में (i) से भाग देने पर,
दे-ब्रॉग्ली तरंगदैर्ध्य λ=λ0[1+eE0mV0t]
Topper's Solved these Questions
Similar Questions
एक स्प्रिंग (कमानी) का कमानी स्थिरांक k है। इसको तीन भागों में काट दिया गया है जिनकी लम्बाइयों का अनुपात 1:2:3 है। इन तीनों भागों को श्रेणी क्रम में जोड़ने पर, संयोजन का कमानी स्थिरांक k' तथा समान्तर क्रम में जोड़ने पर k" है तो अनुपात k':kk" होगा:
View Solution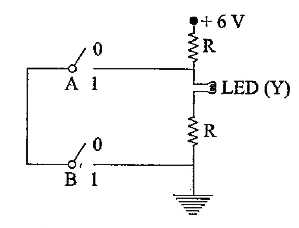
आरेख के परिपथ द्वारा निरूपित सही बुलियन प्रचलन है
View SolutionA portion is fired from origin with velocity →v=v0ˆj+v0ˆk in a uniform magnetic field →B=B0ˆj. In the subsequent motion of the proton
View SolutionAn electron of mass m with an initial velocity vec(v) = v_(0) hat (i) (v_(0) gt 0) enters an electric field vec(E ) = v_(0) hat (i) (E_(0) = constant gt 0) at t = 0 . If lambda_(0) is its de - Broglie wavelength initially, then its de - Broglie wavelength at time t is
View SolutionElectric field strength bar(E)=E_(0)hat(i) and bar(B)=B_(0)hat(i) exists in a region. A charge is projected with a velocity bar(v)=v_(0)hat(j) at origin , then
View SolutionAn electron (mass m) with an initial velocity v=v_(0)hat(i)(v_(0)gt0) is in an electric field E=-E_(0)hat(l)(E_(0)="constant"gt0) . Its de-Broglie wavelength at time t is given by
View Solutionआरम्भिक वेग →v=v0ˆi(v0>0) और द्रव्यमान m का कोई इलेक्ट्रॉन किसी वैधुत क्षेत्र →E=−E0ˆi (E0= स्थिरांक >0 ) में t= 0 पर प्रवेश करता है । यदि प्रारम्भ में इस इलेक्ट्रॉन की दी-ब्रोगली तरंगदैर्घ्य λ0 है , तो समय t पर इसकी दी-ब्रोगली तरंगदैर्घ्य होगी :
View SolutionAn electron (mass m) with an initial velocity vec(V) = v_(0) hat(i) is in an electric field vec(E) = E_(0) hat(j) . If lamda_(0) = (h)/(mv_(0)) , its de Broglie wavelength at time t is given by
View SolutionAn electron of mass m with an initial velocity →V=V0ˆi(V0>0) enters an electric field →E=−E0ˆi (E0 = constant >0) at t = 0. If λ0 is its de Broglie wavelength initially, then its de Broglie wavelength at time t is
View SolutionAn electron is projected wit velocity →v=v0ˆx in an electric field →E=E0ˆy. Trace the path followed by the electron :-
View Solutionयदि A और B दो स्वतंत्र घटनाएँ इस प्रकार है जैसे की P(A)>0 और P(B)>0।, तो
View Solutionएक इलेक्ट्रॉन अपने प्रारम्भिक वेग v=v0ˆi के साथ वैघुत क्षेत्र E=E0ˆj में विघमान है। यदि λ0=hmv0 हो, तो इसकी दे-ब्रोग्ली तरंगदैर्ध्य t समय पर होगी
View Solutionकिसी विधुत क्षेत्र →E=E0ˆy में एक इलेक्ट्रॉन को →v=v0ˆx वेग से प्रक्षेपित किया जाता है। इलेक्ट्रॉन द्वारा अनुरेखित पथ होगा :-
View SolutionAn electron (mass m) with an initial velocity v=v0ˆi(v0>0) is in an electric field E=−E0ˆl(E0=constant>0). Its de-Broglie wavelength at time t is given by
View SolutionThe acceleration of a particle is given by vec(a) = [2 hat(i) + 6t hat(j) + (2pi^(2))/(9) cos ((pi t)/(3)) hat(k)] ms^(-2) . The initial conditions are vec(r ) (0) = x(0)hat(i) + y(0) hat(j) + z(0) hat(k) = vec(0), vec(v) (0) = (2 hat(i) + hat(j)) ms^(-1) wher vec(v) (0) = (d hat(i) (0))/(dt) = (dx (0))/(dt) hat(i) + (dy(0))/(dt) hat(j) + (dz(0))/(dt) hat(k) The position vector at t= 2 s is
View SolutionAn electron (mass m) with an initial velocity v=v0ˆi(v0>0) is in an electric field E=−E0ˆl(E0=constant>0). Its de-Broglie wavelength at time t is given by
View Solution
